LE CERCLE UNIVERSEL DE NAVIGATION
DE BOISSAYE DU BOCAGE
Un abaque de marine normand
en usage à la fin du XVII^e siècle

"Sous le règne de Louis XIV, la Marine de France fut très florissante."

Jérôme Lalande – "Abrégé de navigation, historique, théorique et pratique" – 1793.

Le "Cercle universel" de Georges Boissaye du Bocage, "hydrographe entretenu de sa Majesté", est un abaque permettant au marin de résoudre, sans table et sans calcul, différents problèmes liés à la navigation. Sans réelle originalité propre, il est cependant très intéressant par la tentative de synthèse qu'il représente (on trouve rassemblé dans une seule page tout ce qui existait dans le genre à l'époque) et par les applications très variées qu'en donne l'auteur.

Le "Cercle Universel" (et son usage) est publié pour la première fois en 1683 ("Achevé d'Imprimer pour la première fois le 20 Novembre 1683"), simultanément chez Jacques Gruchet au Havre et chez Nicolas l'Anglois à Paris (1 vol, in-12, VIII – 144 p.).

Il correspond à l'enseignement que donnait l'auteur, et son père, à l'école d'hydrographie du Havre, et dut connaître un certain succès, puisque trois autres éditions de l'ouvrage allaient suivre en 1689, 1695 et 1733.

Description du "Cercle Universel"

Le Cercle Universel figure sur une planche dépliable de 32´40 cm. Le Cercle lui même mesure 30,5 cm de rayon et était, pour être utilisé, collé sur un carton. Une ficelle est fixée à son centre, et il faut avoir un compas à pointes sèches à portée de la main.

Le Cercle est entouré de différents graphiques et échelles accessoires.

Le Cercle Universel

· Les cercles extérieurs constituent un calendrier fournissant, pour chaque jour de l'année, la position du Soleil sur l'écliptique, par ses degrés sur l'échelle zodiacale. Cela équivaut à une table.

· La moitié supérieure est occupée par un demi-astrolabe de Rojas, appelé aussi "sphère plate" ou "quartier sphérique", lorsqu'il est réduit à un quart, ou "quartier astronomique et universel". Il s'agit de la projection orthographique (orthogonale) de la sphère sur un plan tangent à l'équateur. Elle permet de résoudre des problèmes astronomiques liés à la navigation, dont la détermination de l'heure d'après la hauteur du Soleil. L'histoire de cet abaque rejoint celle de l'astrolabe.

La partie du Cercle Universel laissée libre au dessus de la projection de Rojas est occupée par trois schémas : de gauche à droite, cercles montrant le mouvement de l'étoile polaire, cercle montrant l'horizon, le zénith, les pôles, l'équateur… et enfin deux cercles excentrés montrant le périgée et l'apogée du Soleil dans son mouvement apparent annuel.

· Le quart de cercle inférieur droit est un quartier de réduction, nommé aussi "quartier de proportion" ou "quartier d'or". Il permet d'obtenir par exemple la distance parcourue en fonction de la direction suivie et de la différence de latitude.

· Le quart de cercle inférieur gauche reproduit les différentes échelles du compas de proportion. Il s'utilise avec le fil et un compas à pointes sèches, pour effectuer les calculs analogues à ceux que permet cet instrument. On trouve 7 échelles : en 100 parties égales, des cordes des angles (trigonométrie), des plans, des solides, des polygones, des métaux et pierres et enfin de la quille, mâts, etc. (une échelle des diamètres des boulets de canon se trouve à l'extérieur du cercle, tout en bas de la planche).

Au dessus du Cercle

· En haut à gauche, une rose des 32 vents. Les chiffres à l'extérieur indiquent "l'heure qu'il est haute mer dans un havre quand la lune est dans cet air de vent", aux jours de nouvelles et pleines lunes.

· Le schéma à droite explique les phases de la lune.

· Vient ensuite un schéma illustrant le mouvement des étoiles au cours de la nuit.

· En haut à droite, une projection d'Azarquiel et Gemma Frisius de la sphère (projection stéréographique sur le plan du colure des solstices, de pôle le point g) montre comment "il faut placer chaque terre en sa véritable latitude et longitude".

· En dessous de la projection de la sphère, on trouve un calendrier perpétuel "pour trouver par quel jour de la semaine commence chaque mois", semblables à ceux figurant sur les cadrans solaires en ivoire de Dieppe.

En dessous du Cercle

· Au centre une "Eschelle de dime", règle permettant d'apprécier les dixièmes.

· De part et d'autre, un schéma des systèmes de Ptolémée et Copernic.

Sur les côtés

· A droite figure une échelle des "lhogarithmes" et une autre des latitudes croissantes.

· A gauche, une échelle des ombres du Soleil.

L'enseignement de Boissaye du Bocage, père et fils, à l'école d'hydrographie du Havre

La planche du Cercle Universel apparaît comme un résumé graphique des leçons des Boissaye.

Georges Boissaye du Bocage père (1626-1696), originaire des environs de Honfleur, arrive au havre vers 1660, où ses activités ne se limitent pas à celles de maître de pilotage. Il est également ingénieur des constructions navales. C'est ainsi que le 3 décembre 1683 il écrit au ministre de la marine[1] pour "lui remonstrer très humblement qu'il a besoing d'une augmentation d'appointemens pour faire subsister deux de ses enfants qui travaillent journellement avec luy, ne pouvant pas subvenir seul à donner les leçons aux officiers de la marine et aux enfants de la ville, et à faire le toisé des bois [pour la construction navale] et celuy des travaux de la place [aménagements du port et des fortifications]."

Georges Boissaye du Bocage fils (1661-1717) n'a que 22 ans lorsqu'il publie son "Cercle Universel".

Comme il l'indique dans son Avant Propos, pour justifier l'absence de démonstrations mathématiques, "je suis trop jeune & la matière est encore trop délicate pour moy."

Mais il cède aux pressions pour mettre au jour "le peu de connaissance que mon Père m'en a donné".

Au delà du côté publicitaire vantant l'aspect universel de l'instrument, ce qui est assez fréquent, il faut avouer que les exemples d'usage donnés dans le livre touchent à de nombreux corps de métier, ce qui est assez original, et sans doute en rapport avec les diverses activités du père dans les domaines des "mathématiques pratiques".

Les écoles royales d'hydrographie ont été créées en 1661 par Colbert. Boissaye du Bocage père semble être le premier titulaire du poste de professeur d'hydrographie au Havre (on ignore la date de fondation de l'école d'hydrographie du Havre, celle de Dieppe lui est sans doute antérieure).

Le rôle, les droits et devoirs du professeur d'hydrographie ont été rappelés dans l'Ordonnance de la Marine Du mois d'Aoust 1681[2].

On y remarque, en particulier, la définition qui est donnée du mot "hydrographie". Loin de se limiter à la cartographie des zones côtières, l'hydrographie regroupe tout ce qui concerne "l'Art de la navigation". Cependant les professeurs d'hydrographie "sçauront dessigner" et l'on pourra juger des réalisations de Boissaye du Bocage père en examinant sa "Baie de Brest" (numérisation BnF sur http://gallica.bnf.fr ).

Cette même ordonnance de 1681 enjoint aux pilotes "de faire des journaux qui soient justes et de naviguer par latitude et longitude", preuve que la navigation "à l'estime", "par route et distance", est encore fréquente.

En juin 1682 et de nouveau en janvier 1683, Boissaye du Bocage père envoie un mémoire au ministre de la marine montrant que l'enseignement au Havre est conforme aux prescriptions de l'ordonnance de 1681[3]

"Mémoire à Monseigneur de toutes les matières qui sont traittées à l'escole d'hydrographie du port du Havre."

Suit, dans "l'ordre observé par le maître d'hydrographie", le contenu des leçons :

· 1^ère leçon : calcul de l'âge de la lune et de l'heure de la haute mer ; cercles principaux de la sphère avec "démonstration d'iceux sur les globes et cartes".

· Travail avec la règle et le compas, en particulier pour que les élèves puissent "faire leurs instrumens".

· Comment trouver la latitude "au soleil et aux estoilles".

· Variation de l'aimant et travail sur la carte "tant réduite que plate". Détermination et calculs des différents éléments de la route.

· Trigonométrie et logarithmes.

· Usage de l'arbalestrille ("la flesche"), du compas de proportion, du graphomètre, de la tablette, pour faire les cartes.

Boissaye du Bocage va au-delà de ce qu'indique l'Ordonnance :

· S'il se trouve des officiers "qui veulent outre ce que dessus apprendre la fortification, l'arpentage et le toisé, il leur est monstré".

Boissaye du Bocage ajoute (ce qui est particulièrement en rapport avec le Cercle Universel) :

"La manière est donnée de trouver sans calcul touttes les choses dites cy dessus, avec la règle et le compas seullement.

Elles sont de mesme enseignées par l'échelle proportionnelle avec le compas simple.

L'usage des globes et sphères est enseigné, comme aussy celuy de la sphère plate [la projection orthographique de Rojas]."

Pour conclure, le professeur d'hydrographie indique :

"Chaque officier a son cahier particulier sur lequel il escrit les leçons qui luy sont données, et les heures desdites leçons sont partagées à chacun selon le degré où ils se trouvent, et ordinairement l'Escole pour les officiers dure trois heures.

Tout ce qui dessus est monstré les après midy aux Enfans de la ville qui ont pareillement leurs cahiers."

Il semble cependant que l'enseignement de Boissaye du Bocage père soit jugé inférieur à celui donné à Dieppe par le père Guillaume Denys (et sa rémunération inférieure). La situation s'inversera par la suite. Boissaye du Bocage fils obtiendra que la rémunération soit la même au Havre et à Dieppe. Par la suite, l'école d'hygdrographie du Havre occupera la première position en France. C'est le cas à l'époque de Pierre Bouguer (1730).

Les professeurs de l'Ecole Royale d'Hydrographie du Havre de 1666 à 1791
Georges Boissaye du Bocage (père)	1666-1694
Georges Boissaye du Bocage (fils)	1694-1717
Frémont	1717-1726
Meynier	1726-1730
Pierre Bouguer	1730-1735
Duvivier (suppléant de Bouguer)	1735-1737
Aze (suppléant de Bouguer)	1737-1745
Aze	1745-1752
L. Cléron (père)	1753-1772
J. L. Cléron (fils)	1772-1791

Appointements des professeurs royaux d'hydrographie (en livres par an)
	Le Havre	Dieppe
1665		1200
1678	720	1200
1684	900	1200
1694	1050	1050

A son entrée en fonction, en 1694, Georges Boissaye du Bocage, le fils, se plaint de la différence de traitement (300 livres) qui demeure entre Le Havre et Dieppe. La "poire sera coupée en deux".

En 1726, Jacques le Cordier, professeur d'hydrographie en titre à Dieppe, écrit au ministre de la marine (Maurepas) pour lui signaler que le professeur d'hydrographie du Havre "a une classe à l'arsenal où il tient ses écolles et qu'outre ses appointements de mille cinquante livres par an, il jouit encore de trois cents livres de la Ville lui paye pour son logement." Il obtiendra 120 livres payées par la ville de Dieppe comme indemnités de logement.

A côté des professeurs royaux, il existe d'autres professeurs de pilotage, comme Nicolas Corruble (1651-1719), à Dieppe, qui, comme Boissaye du Bocage, publie en 1683.

1683 : de nombreuses publications, au Havre et à Dieppe, concernent la navigation

· Au Havre-de Grâce, chez Jacques Gruchet, paraissent en 1683 les éditions originales de deux traités de Samson Le Cordier (1647-1709), professeur d'hydrographie à Dieppe :

- "Instruction des pilotes".

- "Traité des pratiques journalières des pilotes".

La première est conçue "pour aider les commençans", la seconde est composée "en faveur des experts".

· Toujours chez Jacques Gruchet, parait en 1683 (première édition) "Le pilote expert" de F. Dassier (on ignore le prénom) où l'on explique l'usage de l'échelle de Gunter (logarithmes), ouvrage signalé par Lalande (Abrégé de navigation – Paris 1793). Cependant, d'après Lalande, "[Bion ne] parle point de l'échelle de Gunter, parce qu'elle n'était point employée dans la Marine française."

· Chez le même Jacques Gruchet paraît en 1683 une nouvelle édition de l'ouvrage de Guillaume Blondel (la première édition est de 1671) : "Le véritable art de naviguer par le quartier de réduction, avec lequel on peut réduire les courses des vaisseaux en mer, et enrichi de plusieurs raretez qui n'ont point encore été découvertes".

Blondel y affirme que le quartier de réduction "est en grande estime à présent par tout, pour les curieuses et rares observations qui se pratiquent sur iceluy en mer" mais qu'aucun auteur n'a encore écrit sur son usage.

Blondel avait fait paraître en 1680, chez Jacques Gruchet (1^ère édition), "L'art de naviguer par le compas de proportion". Il y espère que cet instrument, appliqué à la navigation, ne sera pas moins estimé que son "Quartier de réduction".

· En 1683 paraît à Dieppe, chez Nicolas Dubuc, l'ouvrage de Nicolas Corruble : "La véritable et unique méthode de naviguer par le quartier d'Or laquelle est prouvée d'une manière si facile et démontrée par des figures si claires et si intelligibles d'elle mêmes que l'on pourra sans peine & en peu de temps se rendre parfait Pilote & faire une heureuse navigation". L'auteur affirme dans sa préface que ces quartiers (il s'agit de quartiers de réduction) "se trouvent es mains de tous nos navigateurs".

D'autres instruments de calculs du marin

Les pilotes ont longtemps préféré les abaques plutôt que l'usage de tables, ou, à plus forte raison, que le calcul par trigonométrie et logarithmes. L'œuvre de Boissaye du Bocage s'inscrit dans une longue tradition d'instruments plus ou moins "universels" dérivés généralement de l'astrolabe. En voici quelques exemples.

Aux XVIe et XVIIe siècles

· En 1612 paraît à Paris, "Déclaration, instruction et usage du Pantoscope, ou instrument universel, concernant les observations Astronomiques, Astrologiques, Cosmographiques, Géographiques, Maritimes, Géométriques, Chorographiques, et autres. De l'invention de M. Noël Léon Morgard, Parisien, Mathématicien". L'instrument, dérivé de l'astrolabe, est essentiellement à but astrologique.

· On peut voir au Musée d'Histoire des Sciences d'Oxford ( et sur le site http://www.mhs.ox.ac.uk/database ) une règle à calcul circulaire (circular slide rule) datant environ de 1634 et signée Elias Allen, le constructeur du mathématicien William Oughtred, inventeur de la règle à calcul. L'instrument est en laiton, d'un diamètre de 45 cm.

Les cercles extérieurs, nommés "cercles de proportion" sont des échelles logarithmiques (on les utilisait avec deux index, manquants, jouant le rôle d'un compas à pointes sèches). C'est la première forme des "règles à calcul" qui, avant d'être des règles à coulisses, sont ainsi circulaires. On reconnaît au centre une projection orthographique de la sphère (astrolabe de Rojas).

· Un cercle nautique, également anglais, de la fin du XVIe siècle (signé Charles Whitwell) est visible au Musée d'Histoire des Sciences de Florence. Il est en laiton et mesure 73 cm de diamètre. Il faisait sans doute partie d'un instrument plus complexe, décrit par Robert Dudley dans "Arcano del mare". Il permet différents calculs utiles à la navigation.

On a vu les productions normandes du XVIIe siècle.

D'autres exemples se rencontrent au siècle suivant.

Au XVIIIe siècle

· Benjamin Scott publie à Londres en 1733, "The Description and use of an Universal and Perpetual Mathematical Instrument shewing the most Expeditious and Exact Method of solving all practical questions in Aritmetick, Trigonometry, Navigation, Dyalling, Astronomy, etc…". L'instrument consiste en 20 cercles, 12 arcs de cercles et trois tables.

· Jean-Baptiste Degaulle (1732-1810), professeur de pilotage au Havre, est l'auteur d'un Calendrier perpétuel dont le mode d'emploi est détaillé dans "Usage du nouveau Calendrier perpétuel, astronomique et maritime…" publié en 1768. L'instrument est en carton et mesure 40 cm de diamètre. Il "se vend au Havre chez l'auteur, rue St Jacques, et chez Faure, imprimeur, [dans la même ville] rue St Michel."

On y remarque encore la présence de la projection de Rojas. Ces pièces en carton ont rarement été conservées.

Le "Cosmoplane" de l'abbé Dicquemare (Le Havre 1733-1789) possède certaines similitudes : "Description du Cosmoplane, inventé et construit par M. l'abbé Dicquemare, professeur de physique expérimentale au Havre-de-Grâce" est édité à Paris en 1769.

Usages du Cercle Universel

Trouver la position du Soleil dans le zodiaque

Exemple :

On désire connaître la position du Soleil le 26 mai.

Dans la case correspondant au 26 mai, on lit 5 25. Ce qui signifie que le Soleil est à 5°25' dans le signe des Gémeaux, puisque le symbole des gémeaux est le signe zodiacal précédent (le Soleil entre dans ce signe le 21 mai).

L'auteur précise : "nottez aussi que cette Table est prise pour la deuxième année après Bissexte, n'ayant pû mettre pour les 4 années." En effet les dates des équinoxes et solstices fluctuent à un jour près, la valeur pour la deuxième année suivant la bissextile constituant une moyenne.

L'astrolabe de Rojas

L'astrolabe de Rojas est un astrolabe "universel", c'est-à-dire pour toutes les latitudes, à la différence de l'astrolabe planisphérique standard. Il est obtenu à partir d'une projection équatoriale orthographique de la sphère céleste. Les premiers astrolabes universels, dits d'Arzaquiel ou de Gemma Frisius, ont été obtenus par projection stéréographique sur un plan contenant l'axe de la sphère (plan méridien).

L'astrolabe universel ci-dessous (il en manque la règle, pivotant au centre et munie d'un curseur orthogonal, système remplaçant l'araignée traditionnelle) est intéressant car "double", ce qui permet de comparer les projections : orthographique à gauche et stéréographique à droite. Il est visible au musée d'histoire des sciences de Florence.

La projection équatoriale orthographique consiste à projeter la sphère orthogonalement, sur un plan tangent à l'équateur. Les parallèles sont représentés par des droites, de plus en plus serrées vers les pôles, les méridiens par des arcs d'ellipse. Cette projection ne conserve ni les distances ni les angles, mais elle correspond à une vision de la sphère vue de très loin (en fait d'un "point" situé à l'infini).

Vue de la terre en projection équatoriale orthographique :

La projection équatoriale stéréographique est une projection stéréographique de la sphère sur un plan tangent à l'équateur dont le pôle est diamétralement opposé au point de tangence.

Parallèles et méridiens sont représentés par des arcs de cercles (l'équateur et le méridien central sont des droites). Puisque c'est une projection stéréographique, elle conserve les angles et l'on peut représenter plus qu'un hémisphère.

Vue de la terre en projection équatoriale stéréographique :

La projection stéréographique utilisée pour les astrolabes universels est un peu différente. Elle se fait sur un plan contenant l'axe des pôles (plus précisément sur celui que l'on nomme des colures des solstices, c'est à dire passant par la position du Soleil aux solstices).

L'origine exacte de l'utilisation de la projection stéréographique, dans la recherche d'un astrolabe universel, n'est pas certaine. Aux IXe et Xe siècle apparaissent au Moyen-Orient des "tables d'horizon" dont le principe va dans ce sens. Ce qui est sûr, c'est qu'au XIe siècle, à Tolède, deux astronomes contemporains travaillent sur un astrolabe universel obtenu par projection stéréographique.

Le premier, peu connu, Ali ben Khalaf ben Ahmar écrit[4] :

"… il arriva que je compris comment peut être fait un instrument [astrolabe] pour le monde entier, qui ne contiendrait pas plus d'un tympan et une araignée. Je lui est donné le nom d'horizon universel, et l'ai réalisé pour mon seigneur le roi Ma'mun [de Tolède A.D. 1037-1074] et ai fait ce livre…"

Il s'agit d'une matrice sur laquelle est gravée une projection stéréographique sur le colure des solstices, sur laquelle tourne une araignée divisée en deux parties, une moitié constitue une carte des étoiles, l'autre moitié une toile de méridiens et parallèles.

Plus célèbre, même de son temps, Ibn az-Zarquellu (Azarquiel ou Arzachel ou Arzaquiel), né à Cordoue mais qui vécut surtout à Tolède (le pont principal enjambant de nos jours le Tage porte son nom), conçoit sa saphea. Il abandonne l'araignée (seule subsiste la matrice) mais ajoute une alidade munie d'un curseur avec un petit bras. En 1263 Profatius de Montpellier (Ibn Tibbon) rédige, avec l'aide de Jean de Brescia, une version latine, à partir de la traduction en hébreu qu'il a effectuée du texte arabe d'Azarquiel.

C'est cette même saphea que reprend Gemma Frisius, vers 1550, pour son "astrolabe catholique". Elle apparaît dès lors souvent, associée à un astrolabe classique, au dos des instruments d'Arsenius.

C'est en 1551 que Juan de Rojas Sarmiento, élève de Gemma Frisius, publie son Commentarium in astrolabium, conservant le plan du colure des solstices comme plan de projection, mais rejetant le pôle de projection à l'infini, autrement dit, effectuant une projection orthographique. De Rojas n'est cependant pas à l'origine de cet instrument (et n'affirme pas l'être) ni, à plus forte raison de cette projection.

On ne connaît pas l'origine précise de la projection orthographique, mais Hipparque (vers 150 av. J.-C.) l'utilise dans ses analemmes [5]. Il s'agit d'une technique permettant, par projection orthographique sur un plan méridien et rabattement de cercles de la sphère, de résoudre par la trigonométrie plane un problème de l'espace (la trigonométrie sphérique n'est pas connue). Al Biruni mentionne cette projection dans son traité de l'astrolabe. Oronce Finé, dans son Promathesis (1532) donne une brève description (avec illustration) d'un cadran solaire utilisant cette projection orthographique. Enfin des astrolabes de type "Rojas" existent bien avant que Juan n'en parle : deux instruments, attribués à Hans Dorn de Vienne, datant de 1480 et 1483, nous sont parvenus[6] (visibles en Pologne).

La lecture de la projection utilisée par Rojas semble plus facile que celle de la saphea d'Arzaquiel (voir l'instrument de Florence). Cependant l'utilisation de l'astrolabe universel est plus compliquée et, surtout, on a perdu les qualités pédagogiques qui faisaient de l'astrolabe classique une maquette de l'Univers. Toutefois, l'astrolabe universel est particulièrement adapté à certains problèmes : la projection peut représenter, selon l'interprétation que l'on en fait, les coordonnées d'un point du ciel dans les trois systèmes, coordonnées locales, équatoriales et écliptiques, ce que ne fait pas l'astrolabe classique (d'où leur association dans les astrolabes d'Arsenius).

Appliqué à la navigation, l'astrolabe de Rojas prend le nom de "sphère plate", réduite à un demi-hémisphère dans le Cercle Universel (l'écliptique est rabattu par symétrie) ou de "quartier sphérique" dans le cas d'un quart d'hémisphère.

Voici ce qu'en dit le père Esprit Pézenas dans l'Astronomie des marins, ou nouveaux éléments d'astronomie à la portée des marins (Avignon 1766) :

"Le quartier de réduction me paraît trop mystérieux, lorsqu'on l'applique à la solution des Problèmes Astronomiques ; je ne perdrai pas mon temps à développer ces mystères. Le Quartier sphérique vaut mieux. J'avais substitué à cet instrument le demi-cercle sphérique, qui est beaucoup plus commode que le quartier sphérique. Celui-ci est fondé sur la projection orthographique, et le demi-cercle sphérique est un développement de la projection stéréographique, dont les Anglois font beaucoup de cas. Ces opérations subsidiaires peuvent aider, diriger, et même rectifier le calcul."

Et plus loin, à propos de la projection orthographique : "Cette projection a fait naître la Quartier sphérique qui est entre les mains des Marins. C'est ordinairement le quart de la projection orthographique de plusieurs cercles de la sphère sur le plan d'un Méridien. On l'inscrit dans un quarré, dont deux côtés divisés par des transversales, servent à distinguer les minutes du quart de cercle, en étendant jusqu'à ces divisions le fil attaché au centre du Quartier. […] On en trouve de gravés beaucoup plus grands [que celui gravé dans l'ouvrage]. […] Il y a des problèmes d'Astronomie que l'on résoud [sic] fort aisément et avec assez d'exactitude par le moyen du quartier sphérique ; on en résoud même plusieurs par la seule inspection. Son plus grand défaut consiste en ce que les degrés deviennent trop petits en s'éloignant du centre de projection, en sorte qu'on ne peut plus les distinguer aux extrémités. […] Ces projections sont très utiles pour vérifier les calculs astronomiques."

Passons à la pratique.

Trouver la déclinaison du Soleil

Le calendrier zodiacal extérieur a fourni la position du Soleil sur l'écliptique (longitude céleste) : le 26 mai, 5°25' Gémeaux. Il s'agit maintenant de lire sur la demi-sphère les coordonnées équatoriales du Soleil. On repère la position du Soleil sur l'écliptique gradué tous les degrés de longitude céleste (on est en haut à gauche, assez proche du solstice d'été).

Il suffit de voir quel parallèle rencontre l'écliptique à ce point. Les parallèles correspondent aux droites horizontales, tous les degrés, en gras tous les 5 degrés. On voit qu'on est un peu au-dessus du 21^ème parallèle. D'où la déclinaison du Soleil d = 21° 1/3.

En examinant le méridien céleste croisé à 5°25' Gémeaux, on aura l'ascension droite. Les arcs méridiens sont tracés tous les 5°, avec une graduation tous les degrés le long de l'équateur (diamètre horizontal). On lit environ a = 63° d'ascension droite. Attention, le Soleil parcourt deux fois au cours de l'année chaque segment d'écliptique représenté, et on est au premier quart (l'origine est fixée à l'équinoxe de printemps).

Trouver l'heure du lever et du coucher du Soleil

En premier exemple, Boissaye du Bocage se situe à la latitude j = 50° , approximativement celle de Dieppe, un jour où la déclinaison du Soleil est d = 16°. On peut rechercher quel jour on est. Le 16^ème parallèle coupe l'écliptique, dans la partie gauche en été, et dans la partie droite en hiver. On utilise ensuite le calendrier zodiacal. Mais ce n'est pas la question, on veut connaître les heures de lever et coucher du Soleil. On supposera qu'on est en été, car sinon, n'ayant qu'une demi-sphère, tout est à l'envers (rabattement par symétrie), ce qui, au départ, trouble un peu.

Le fil va nous servir à représenter la projection du plan de l'horizon local. Ce plan fait, avec l'axe des pôles, un angle égal à la latitude, soit 50° (hauteur approximative de la polaire au-dessus de l'horizon).

On tend donc le fil sur la graduation 50, située en haut à gauche, sous le calendrier zodiacal.

Au cours de la journée, le parcours du Soleil se fait sur le parallèle de 16°. Quand il est en dessous de l'horizon il fait nuit (plus ou moins). Il faut donc considérer l'intersection du 16^ème parallèle céleste avec le fil horizon et regarder "droit en haut" (en fait en tournant un peu pour suivre la courbure des méridiens) à quel méridien cela correspond. En haut, sur le tropique, les méridiens sont gradués en heures (une heure pour 15°), toutes les 4 minutes. On lit 4h40 ou 7h20 (on est à peu près sur un méridien tracé : 20° et 160° d'ascension droite) pour le lever et le coucher (il y a une double graduation en heure, correspondant à l'aller-retour du Soleil sur son parallèle projeté).

Boissaye du Bocage lit 4h41, il doit confondre son Cercle Universel avec un chronomètre !

Pour la position symétrique, en hiver, il suffit d'inverser le jour et la nuit (et là l'auteur renonce à sa minute de précision).

Trouver l'heure d'après la hauteur du Soleil dans le ciel

Ici, cela se complique un peu. Le compas à pointes sèches entre en scène. Le fil-horizon jouant le rôle de la règle de l'astrolabe de Rojas, le compas fera fonction de curseur orthogonal, l'expression la "pointe ne fasse que razer le filet" signifiant de faire en sorte que l'arc de cercle soit tangent au fil (pour l'orthogonalité).

Dans l'exemple choisi, l'auteur suppose toujours que l'on se situe à la latitude j = 50°, que le Soleil a une déclinaison d = 21°41'. On sait comment figurer ces données sur l'instrument. On observe maintenant que le Soleil est à une hauteur h = 15°20' au-dessus de l'horizon. Le problème consiste à repérer cette hauteur sur la projection, ne disposant pas des cercles d'égale hauteur (al mucantarat) de l'astrolabe classique.

C'est là que l'on va comprendre l'avantage de l'astrolabe universel. Si l'on disposait, au lieu du fil, d'une double grille pivotante, il suffirait de la faire tourner pour se situer à 50° de latitude. Mais une telle grille serait fragile et peu précise, on va y suppléer avec le fil et le compas.

On place le fil correspondant à un horizon de latitude 50°. Le parcours du Soleil se faisant, dans la journée, sur le parallèle de déclinaison 21°43'.

Avec le compas (faisant comme si l'on observait à l'équateur), on prend sur l'équateur un écartement correspondant à la distance entre le centre du Cercle et le méridien situé à 15°20'. Puis on se débrouille pour reporter cette distance entre le fil horizon et le trajet du Soleil de sorte à avoir un angle droit avec l'horizon : on est sensé déplacer et pointer le compas sur le parallèle du Soleil et le faire tourner de façon à trouver la position ou le cercle décrit par la seconde pointe semble tangent au fil.

La position du compas étant trouvée sur le parallèle de déclinaison 21°43', il suffit alors de lire l'heure sur le méridien correspondant. La position du Soleil obtenue est un peu avant la ligne de 6 heures. On lit 5h52 si on est le matin et 6h08 si on est le soir. Avec une ficelle et un compas à pointes sèches, la méthode n’est pas très précise. La belle figure qui suit, réalisée par Armin Zenner (Dormagen – Allemagne), montre plus exactement la situation.

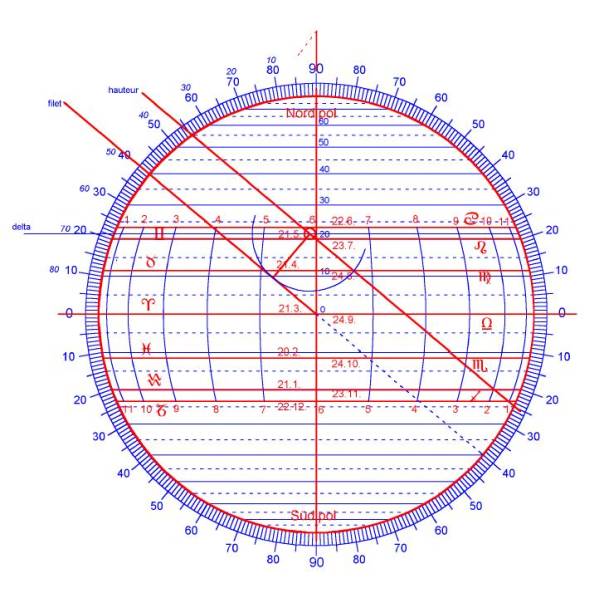
Déterminer la position du navire

Le problème central de la navigation, la tâche du pilote, est celui de la détermination de la position du navire en mer. Quatre paramètres interviennent dans cette question, la connaissance de deux d'entre eux étant a priori suffisante pour connaître la position.

Supposons que le bateau, parti du point A, se trouve au point B.

· La "route" V, est l'angle que fait AB avec la direction du Nord. Cet angle, le cap suivi par le bateau, est donné par la boussole, le "compas" de marine. Cette mesure est cependant peu précise. Le pilote doit tenir compte de la précision toute relative de la rose des vents, des changements de cap, des courants…

· Le "chemin" est la distance AB parcourue, généralement exprimée en milles marins. Elle est estimée à partir de la vitesse du bateau (mesurée à l'aide du loch) et de la durée de navigation. Cette donnée est assez peu fiable, dans la mesure ou la vitesse propre du navire est difficile à mesurer (courants marins, état de la mer…), sans parler de la mesure du temps en mer au XVIIe siècle.

· La différence de latitude Dj entre A et B est mesurée par la hauteur du Soleil ou d'une étoile au-dessus de l'horizon. Cette mesure est assez simple à effectuer et plutôt fiable, même. D'abord obtenue, à partir du XVe siècle, au quadrant ou à l'astrolabe, elle est prise, au XVIe siècle, à l'arbalestrille (bâton de Jacob) ou, mieux, au quartier anglais ou quartier de Davis, avant l'apparition de l'octant au XVIIIe, puis du sextant.

· La différence de longitude Dl entre A et B est plus difficile à connaître en mer. Les méthodes astronomiques, celle des distances lunaires en particulier, se développent au XVIIe mais, nécessitant des calculs compliqués, elles ne sont à la portée que d'une élite. Il faudra attendre la mise au point des chronomètres de marine.

La navigation "à l'estime" est celle qui est basée sur l'estimation de la "route" et du "chemin". En cette fin de XVIIe siècle, la majorité des pilotes naviguent à l'estime, soit par route et chemin, soit par latitude et chemin. L'Ordonnance de 1681 incite les pilotes à la navigation astronomique, par latitude et longitude.

La longitude est difficile à connaître au XVIIe siècle, mais connaissant AB et Dj ou V et Dj, il est possible d'estimer Dl . On peut procéder par calcul trigonométrique (hors de porté d'une majorité de pilotes) ou à partir de la carte en reportant l'angle V si elle est réalisée selon la projection de Mercator (elles sont encore rares et l'habitude de cette projection est loin d'être entrée dans les mœurs des marins)… ou encore en utilisant des abaques, comme ceux du Cercle Universel. Ce sera longtemps le moyen préféré des pilotes.

Examinons les relations existant entre les quatre paramètres ci-dessus.

L'unité de longueur sera le mille marin, ou la lieue marine. Un mille marin est égal à la distance parcourue sur la sphère terrestre le long d'un grand cercle, pour un angle au centre d'une minute.

Un degré de latitude correspond donc à 60 milles (un méridien est un grand cercle) :

· 1° de latitude = 60 milles = 20 lieues marines (= 1852 m).

En revanche, un parallèle, mis à part l'équateur, n'est pas un grand cercle et il est facile de voir qu'un degré de longitude parcouru à la latitude j correspond à une distance de
60 ´ cos j milles :

· 1° de longitude à la latitude j = 60 cos j milles.

Dans le triangle rectangle ABC, la trigonométrie (plane) donne :

BC = AB cos V , d'où la différence de latitude :

si AB est exprimée en milles.

Par ailleurs, la relation AC = AB sin V fournit approximativement la différence de longitude :

en prenant la "latitude moyenne" j_m entre A et B . Cette "latitude moyenne", ou "moyenne parallèle" n'est pas exactement la moyenne arithmétique des latitudes de A et B. Elle est prise sur "l'échelle des latitudes croissantes" (échelle régulièrement dilatée d'un coefficient 1/cosj ) en considérant le milieu entre les graduations des latitudes de A et B.

Si l'on souhaite éliminer AB, on fait le quotient des relations précédentes :

Cette formule permet de calculer la longitude, connaissant la latitude et l'angle de route.

Les échelles du compas de proportion

Les calculs trigonométriques précédents peuvent s'effectuer en utilisant l'échelle des "cordes" du compas de proportion.

La corde d'un angle est la première ligne trigonométrique à avoir été utilisée. On la doit à Hipparque et on constate qu'elle est encore privilégiée en cette fin de XVIIe siècle. Le sinus, le cosinus et la tangente nous viennent des arabes (le sinus emprunté aux indiens).

Pour l'angle x = AÔM visible sur le cercle trigonométrique ci-contre, la corde est la distance AM :

crd x = AM.

En considérant la corde MM ', correspondant à un angle au centre 2x, on a immédiatement la relation fondamentale suivante :

crd (2x) = 2 sin x .

Le sinus d'un angle est donc lié à la corde de l'angle double. On obtiendra le cosinus comme égal au sinus de l'angle complémentaire à 90°.

Résolution d'un triangle

Commençons, en suivant Boissaye du Bocage, par la résolution d'un triangle dont on connaît deux angles (donc les trois angles) et un côté, à l'aide des échelles "parties égalles" et "cordes" du compas de proportion.

L'auteur considère l'exemple d'un triangle ABC avec : Â = 71°15', = 36°10' et BC =68 toises 2/3.

On demande AC.

Utilisant la loi des sinus, nous écririons : ,

d'où AC = ,

ou encore, en utilisant les cordes (avec crd (2x) = 2 sin x ) :

AC = .

La manipulation, décrite par l'auteur, consiste à reproduire sur le Cercle Universel, à l'aide du compas à pointes sèches et du fil, la configuration de Thalès suivante.

D'après le théorème de Thalès, la proportion sur les côtés parallèles est la même que celle mesurée sur l'échelle des cordes :

Ainsi, la longueur l sur cette figure est bien la valeur AC demandée.

On procède ainsi :

1. On prend au compas un écartement de 68 2/3 sur l'échelle des parties égales.

2. On plante une pointe du compas sur la graduation 142°30' (à peu près) de l'échelle des cordes et la seconde pointe en suivant les cercles concentriques de l'abaque.

3. On tend le fil sur la seconde pointe du compas.

4. On prend au compas l'écartement l entre la graduation 72°20' de l'échelle des cordes et le fil, en suivant les cercles concentriques de l'abaque.

5. On lit la valeur de cet écartement sur l'échelle des parties égales : on trouve 43 (toises).

On peut conserver la même position du fil pour trouver le troisième côté du triangle. Il suffit de venir lire l'écartement du compas entre la graduation 145°10' (c'est 2 = 2 ´ 72°35') de l'échelle des cordes et le fil.

Application à la navigation

L'auteur nous dit que, sachant maintenant résoudre les triangles, on peut passer à un exemple dans le cadre de la navigation.

Soit A le point de départ, à la latitude 40°N, et B le point d'arrivée, à la latitude connue de 42°N. On a suivi une route au Nord Nord-Est, c'est à dire que l'angle V , avec la direction du nord, vaut V = 22°30' (un quart de 90°).

Détermination du chemin

On prend comme unité de longueur la lieue marine (20 lieues pour un degré de grand cercle).

On peut procéder au calcul suivant :

lieues.

Boissaye du Bocage préfère résoudre la triangle ABC dans lequel l'angle en C vaut 90°, l'angle en B vaut 67°30' et le côté AC = 2 ´ 20 = 40 lieues marines (puisqu'il correspond à deux degrés de latitude).

On prend donc au compas un écartement de 40 sur l'échelle des parties égales, que l'on reporte à partir de la graduation 135° (c'est à dire 2´67,5) de l'échelle des cordes en suivant les cercles concentriques. On tend le fil sur la seconde pointe du compas, puis on prend l'écartement entre la graduation 180° (c'est à dire 2´90) de l'échelle des cordes et le fil. Cet écartement correspond à la valeur 43,5 sur l'échelle des parties égales.

On retrouve donc par l'abaque AB » 43,5 lieues marines.

Différence de longitude

La latitude moyenne du trajet est 41°N (on lit pratiquement la moyenne arithmétique sur l'échelle des latitudes croissantes).

Par le calcul on ferait :

L'auteur poursuit la résolution du triangle ABC, en recherchant maintenant la longueur BC.

On reprend la position précédente du fil, obtenue avec un écartement de 40 parties égales à partir de la graduation crd(135°).

On mesure cette fois l'écartement entre la graduation crd(45°) (c'est à dire 2´22,5) et le fil. On trouve que cet écartement correspond, sur l'échelle des parties égales, à BC » 17 lieues.

Reste maintenant à "réduire les lieues en degrés" (de longitude).

Pour cela, la formule est : .

On se ramène à des cordes par :

cos 41 = sin (90 – 41) = sin 49 = = .

Ainsi, .

L'opération s'obtient graphiquement par proportions de Thalès.

On prend au compas 17 parties égales, que l'on reporte à partir de la graduation 98° de l'échelle des cordes, en suivant un cercle concentrique. On tend le fil selon la seconde branche du compas. L'écartement entre l'extrémité de l'échelle des cordes (crd 180°) et le fil, ramené sur l'échelle des parties égales, donne 22,5 lieues.

Il reste à diviser 22,5 par 20. Ce qui donne 1,125 soit 1°7' de différence de longitude.

Le quartier de réduction

Boissaye du Bocage ne dit rien sur le quartier de réduction, renvoyant au "Livre de Monsieur Blondel".

Guillaume Blondel publia pour la première fois en 1679 "Le véritable art de naviguer par le quartier de réduction" dans lequel il affirme que le quartier de réduction "est en grande estime à présent partout, pour les curieuses et rares observations qui se pratiquent sur iceluy en mer" mais qu'aucun auteur n'a encore "écrit sur son usage". L'usage du quartier de réduction fut semble-t-il assez populaire dans la Marine Française. On lit ainsi, dans une édition de 1826 du Traité de Navigation de C.-F. Fournier, que "la méthode du quartier [de réduction], quoiqu'une des moins exactes [par rapport au calcul par exemple] , est fort usitée à cause de sa simplicité, et parce que d'ailleurs il faudrait que la route fût d'une certaine grandeur, et qu'elle se trouvât par une grande latitude, pour que cette méthode fût sujette à des erreurs considérables."

Comme on le voit, le quartier de réduction n'est autre qu'un rapporteur de 90°, quadrillé régulièrement et complété de cercles concentriques pour facilité les reports. Il permet d'effectuer graphiquement les opérations trigonométriques et est un descendant du quadrant des sinus figurant au dos de nombreux astrolabes.

L'utilisation du quartier de réduction consiste à y reproduire un triangle semblable à celui de la navigation. Reprenons l'exemple donné précédemment.

On place A au centre du Cercle Universel. La différence de latitude est de 2°, c'est à dire 2´20 = 40 lieues marines. Plaçons le point C sur le côté du quartier, à 20 carreaux de A (on fait le choix que 1 carreau représente 2 lieues). En prenant un angle en A de 22°30', on place le point d'arrivée B tel que ACB soit rectangle en C.

On lit le chemin AB parcouru en reportant cette distance (avec l'aide éventuelle du fil) sur le côté du quartier. On lit AB » 43,3 lieues.

Pour connaître la différence de longitude, on doit "réduire" la distance CB à la latitude moyenne j_m = 41° :

En prenant en A un angle de 41°, et en considérant le point D tel que ACD soit rectangle en C, on obtient .

On reporte avec le fil le point D en E sur le bord (AC).

En prenant un angle en A de 21°30', on considère le point F tel que ACF soit rectangle en C.

La longueur EF est telle que : .

Il suffit donc de mesurer EF, à l'aide du quadrillage, pour connaître la différence de longitude.

On lit EF » 22 lieues (distance "réduite" à l'équateur).

D'où une différence de longitude d'environ 1,1° (par définition, on a 20 lieues marines par degré de longitude à l'équateur).

Usages topographiques du Cercle Universel

Boissaye du Bocage exploite de différentes façons la graduation angulaire en quatre fois 90 degrés, des quatre quarts du Cercle Universel.

Niveau

"Ce Cercle peut faire la fonction du Niveau…".

On obtient un niveau (un peu rudimentaire) en pliant en deux le Cercle Universel, en fixant une moitié sur le bord d'une planche ou d'une règle, et en attachant un plomb au bout du fil fixé au centre du Cercle.

En sorte que le fil à plomb "batte sur la ligne perpendiculaire au côté que vous avez couppé [ou plié], vous l'ajusterez à plomb [sur la ligne verticale] en haussant ou baissant ladite Table ou règle, ensorte que le plomb vienne comme il a été dit ; Cecy nous servira pour voir si un lieu est plus haut ou plus bas qu'un autre, en regardant le long de la règle ou Table qui doit viser le lieu proposé."

Théodolite

Il s'agit ici de mesurer des angles verticaux. C'est une utilisation classique de l'astrolabe, tenu verticalement. Il manque cependant l'alidade à pinnules. L'auteur la remplace par le fil et deux "équerres" de papier.

"Une perpendiculaire de papier se fait ainsi ; prenez un morceau de papier pliez-le en deux, & replier ce papier doublé en deux autres, ensorte que les bords du plié soient l'un sur l'autre."

Je comprends qu'un fois le papier plié en deux, on plie à nouveau pour former un triangle rectangle, qui sera relevé, le surplus formant une languette d'attache.

"Ayant donc placé comme il a été dit une perpendiculaire au centre [fixée], ayez-en une autre que vous hausserez ou baisserez de votre main ensorte que vous voyez par l'Equaire ou Perpendiculaire qui est au Centre, le couppeau de la Tour [dont on mesure la hauteur] en ligne droite par l'autre Equaire ou Perpendiculaire, pour lors bandez le filet selon la ligne droite par ces deux perpendiculaires, & l'arrêtez ferme-là."

Il doit falloir un peu d'entraînement pour y parvenir avec deux mains…

Graphomètre

On mesure des angles horizontaux, par la même procédure que précédemment, mais avec, cette fois, le cercle posé horizontalement, sur une planchette par exemple.

"Cette manière peut servir pour faire la Carte d'un Païs.

Vous leverez tout plan par cette voye en prenant l'ouverture des Angles. Enfin ce cercle servira de Graffomettre."

Variation de la boussole

Pour savoir quelle est la déviation magnétique, il faut connaître la direction du vrai nord, c'est à dire tracer une ligne méridienne. La méthode proposée par Boissaye du Bocage, utilisant le cercle Universel, est celle des "cercles indiens". Cette méthode est décrite dans le Surya Siddhanta, un ouvrage astronomique datant d'environ 400 av. J.-C.. Cette méthode était très employée par les Arabes et on la trouve en Europe dans les écrits de Gerbert.

"Vous trouverez la Variation de la Boussole avec iceluy [le Cercle Universel] facilement, par deux observations qu'il vous conviendra faire,, autant devant qu'après midy, en cette sorte.

Placez votre cercle sur un Plan parallèle à l'horison, qui vous sera aisé de placer avec votre Cercle qui vous est un Niveau.

Arrêtez bien votre Cercle afin qu'il ne change point [le fixer], tournez le Zénith vers le midy [c'est à dire le haut du Cercle approximativement vers le sud], où l'extrémité de l'ombre de votre Perpendiculaire (qui doit être couppée quarrément) [il s'agit d'un gnomon vertical, à la pointe bien nette, placé au centre du Cercle Universel] vient toucher plusieurs de ces Cercles [il s'agit des cercles concentriques tracés dans la demi-portion inférieure du Cercle Universel] , & y faites des points à toutes les extremitez de l'ombre devant midy.

Après midy remarquez comme devant où l'extremitez de l'ombre de votre Perpendiculaire viendra toucher les mêmes Cercles cy-devant touchez, qui sera autant après midy comme devant midy, faites des points à toutes ces extremitez d'ombres, divisez en deux également l'intervale des points des deux ombres, devant & après midy, par une ligne droite qui passera par le centre, & placée sur cette ligne ainsi tirée, une Boussole où le côté d'icelle soit sur ladite ligne tirée ou parallèle à icelle, pour lors vous verrez si votre Eguille est Parallèle au Méridien. Mais si l'Eguille Aimentée fait un Angle avec ladite ligne, c'est marque qu'il y a de la Variation, & vous verrez de quel côté c'est."

Le schéma résume la procédure.

Calendrier perpétuel

En haut à gauche du Cercle Universel figure une table de nombres constituant un calendrier perpétuel pour connaître le jour de la semaine.

"Il faut sçavoir que les deux rangées de chiffres qui sont en haut séparez par une grosse ligne traversante, sont pour les 12 mois de l'année. Que le mois de Mars est compté pour le premier ; Avril pour le second ; May le troisième &c."

Les jours de chaque mois (jusqu'à 31) sont regroupés en sept colonnes en dessous.

Les quatre dernières cases en bas à droite ne servent à rien et auraient pu rester vides. L'auteur en a profité pour rappeler les numéros des mois de 30 jours (2=avril, 4=juin, 7=septembre, 9=novembre).

Le chiffre de chaque mois indique, dans les deux premières lignes, la colonne correspondant à un jour fixé de la semaine, pour l'année en cours. Ainsi, pour 1683, date de parution du livre, ce jour est le dimanche.

Pour le mois de mars (n°1) 1683, le dimanche est en 7^ème colonne : les 7, 14, 21 et 28 mars 1683 sont des dimanches.

Pour le mois de d'octobre (n°8) 1683, le dimanche est en 3^ème colonne, donc le lundi en 4^ème colonne etc.

"En l'année suivante on haussera d'un jour, mais en l'Année Bissextile on haussera de deux jours, comme en 1682, tous les mois étaient estimez pour Samedys. Qu'en 1683 tous les mois sont estimez pour Dimanche, mais en 1684 il faudra sauter de deux jours partant tous les mois seront des Mardys."

Exemple : à quel jour correspond le 24 août 1684 ?

Le mois d'août correspond au n°6 qui est dans la première colonne qui indique donc le mardi. Le jour n°24 est dans la 3^ème colonne. Le 24 août 1683 est donc un jeudi.

Cela fonctionne encore en 2004 !

Le 7 mars 2004 est un dimanche (voir un calendrier 2004). C'est donc la position du dimanche que donne en 2004 le n° du mois dans le calendrier perpétuel.

Quel jour de la semaine correspond au 18 septembre 2004 ? Le mois n°7 est en 5^ème colonne. Cette colonne est donc celle des dimanches de septembre 2004. Le 18 septembre est en 4^ème colonne, c'est donc un samedi.

Quel jour de la semaine correspond au 15 janvier 2004 ? Attention, dans ce calendrier perpétuel, janvier 2004 est considéré comme le mois n°11 de 2003. Puisque 2004 est bissextile, les n°^s des mois de 2003 indiquent la position des vendredis. Le n°11 est en 2^ème colonne, position des vendredis de janvier 2004. Le 15 janvier est en colonne 1, c'est donc un jeudi.

Il semble que le fait d'affecter le n°1 au mois de mars ait pour but d'éviter l'alternative 28/29 jours du mois de février. C'est donc pour une raison technique que ce calendrier débute au mois de mars et non par conformité à une ancienne tradition (on retrouve que les rangs 7, 8, 9, 10 correspondent à septembre, octobre, novembre, décembre).

La position des mois sur les deux premières lignes se retrouve en raisonnant "modulo 7", durée du cycle hebdomadaire.

mois	n°	Nombre de jours	Reste dans la division par 7	Colonne où doit figurer le mois
Mars	1	31	3	7 (arbitraire)
Avril	2	30	2	7 – 3 = 4
Mai	3	31	3	4 – 2 = 2
Juin	4	30	2	2 – 3 = –1 et –1 + 7 = 6
Juillet	5	31	3	6 – 2 = 4
Août	6	31	3	4 – 3 = 1
Septembre	7	30	2	1 – 3 = –2 et –2 + 7 = 5
Octobre	8	31	3	5 – 2 = 3
Novembre	9	30	2	3 – 3 = 0 et 0 + 7 = 7
Décembre	10	31	3	7 – 2 = 5
Janvier	11	31	3	5 – 3 = 2
Février	12	28/29	Inutile	2 – 3 = –1 et –1 + 7 = 6

Des calendriers perpétuels analogues apparaissent au dos des cadrans magnétiques en ivoire fabriqués à Dieppe dans les années 1660, par Charles Bloud en particulier. Cette fabrication disparaîtra dans les années 1690, du fait d'une déclinaison magnétique devenue trop importante.

La disposition des mois sur les cadrans de Dieppe est analogue, sauf pour les n^os 11 et 12, correspondant à janvier et février, qui sont décalés d'un rang vers la droite. Cela peut permettre d'indiquer, par la position des mois, le même jour de la semaine pour une année civile complète (alors que Boissaye du Boccage applique à janvier et février le jour de l'année précédente). Toutefois, ce ne sera pas valable pour les années bissextiles.

Projection stéréographique de la sphère

En haut à droite du Cercle Universel, figure, à des fins pédagogiques, un planisphère en projection stéréographique.

"Le Cercle qui est à la droite en haut hors des grands cercles, est pour montrer les Méridiens & les Parallèles, & comme il faut placer chaque Terre en sa véritable Latitude & Longitude, & aussi pour faire entendre comme la Latitude se doit compter de la ligne Equinoxiale vers l'un & l'autre Pole, & comme aussi les degrez de Longitude doivent aller en diminuant de valeur, allant vers les Poles.

Vous verrez aussi comme on augmente à compter les degrés de Longitude, allant vers l'Est, & comme on doit soustraire ou diminuer de nombre allant vers l'Ouest, on verra aussi quand il faudra ajoûter en Latitude, ou diminuer selon que l'on s'approche ou éloigne de la ligne Equinoxiale."

Utilisation de l'échelle des logarithmes

On sait que c'est l'écossais John Napier (ou Neper) qui introduisit les logarithmes en 1614 pour simplifier les calculs. La suite de leur histoire se déroule au Gresham College, à Londres, le premier endroit en Angleterre où des chaires de disciplines mathématiques sont instituées pour la promotion de l'astronomie, de la navigation et du commerce. S'y croisent Henry Briggs, professeur de géométrie, Edmund Gunter et William Oughtred.

En 1620 Gunter a l'idée de graduer une règle selon une échelle logarithmique, c'est "l'échelle de Gunter" que l'on trouve ici, à droite du Cercle Universel. Elle s'utilise à l'aide d'un compas à pointes sèches, pour reporter les mesures. Dès 1621, William Oughtred remplace le compas en faisant glisser deux échelles logarithmiques. Il fait réaliser par le constructeur Elias Allen les premières "règles" à calcul (d'abord circulaires). En 1624, Henry Briggs conçoit les logarithmes décimaux, d'utilisation plus pratique.

Alors que les logarithmes, et les règles à calcul, sont très vite utilisés dans la marine Britannique, cela reste beaucoup plus marginal dans la marine Française. Voici ce qu'en dit Lalande dans son Abrégé de navigation (1793) :

"Le calcul des routes par la boussole et le loc, se fait, dans la Marine anglaise, par le moyen de l'échelle de Gunter ou de l'échelle des logarithmes, que nous appelons aussi échelle anglaise. Ce fut en 1624 que Gunter, Professeur au Collège de Gresham, à Londres, proposa cette application importante des logarithmes, dans son livre qui contient la description du Cross-staff ou arbalète. […] on en trouve souvent dans nos ports, tels que Nantes, Dieppe, etc. […] [Bion ne] parle point de l'échelle de Gunter, parce qu'elle n'était point employée dans la Marine française."

Voici cependant un exemple d'utilisation d'une échelle logarithmique pour effectuer des multiplications et divisions à l'aide d'un compas à pointes sèches (il s'agit de jauger la capacité en tonneaux d'un navire).

On sait que les logarithmes transforment les multiplications en additions (réalisées en reportant le compas) :

log(a) ´ log(b) = log(a) + log(b)

et que les logarithmes transforment les divisions en soustraction

log(a / b) = log(a) – log(b).

Ce sont ces propriétés que l'on exploite, à l'aide du compas à pointes sèches.

Dans l'exemple donné par Boissaye du Bocage, la largeur moyenne ("réduite") est 16 pieds, la profondeur moyenne est de 9 pieds et la longueur de 60 pieds.

La capacité, en tonneaux, du navire est donnée par : 16 ´ 9 ´ 60 / 42 » 205,7.

C'est ce calcul que l'on effectue, au compas, sur l'échelle logarithmique.

On prend un écartement entre 0 et 9 au compas, que l'on reporte en avant à partir de la graduation 16. On lit à la seconde branche du compas 144 (environ) qui est 16´9.

On prend un écartement entre 0 et 60 au compas, que l'on reporte en avant à partir de la graduation 144. On lit à la seconde branche du compas 8640 (environ) qui est 16´9´60.

On prend un écartement entre 0 et 42 au compas, que l'on reporte en arrière à partir de la graduation 8640. On lit à la seconde branche du compas 205 (environ).

Le navire jauge environ 205 tonneaux.

Bibliographie

· ANTHIAUME (Abbé Albert) – Evolution et enseignement de la science nautique en France, et principalement chez les Normands – 1920 – BnF cote 8 V 41291.

· D'HOLLANDER (Raymond) – L'Astrolabe, histoire, théorie et pratique – Institut Océanographique 1999.

· D'HOLLANDER (Raymond) – Sciences géographiques dans l'Antiquité – Association Française de Topographie 2003.

· HEBERT (Elisabeth – Sous la direction de) – Instruments scientifiques à travers l'histoire – Ellipses 2004.

· MICHEL (Henry) – Traité de l'astrolabe – Paris réédition 1976.

· Ordonnance de la Marine Du mois d'Aoust 1681 – http//gallica.bnf.fr .

· POULLE (Emmanuel) – Les instruments astron,omiques du Moyen Age – Paris 1983.

· TURNER (Anthony J.) – Early scientific Instruments, Europe 1400-1800.

· TURNER (Anthony J.) – The Time Museum, Time mesuring Instruments.

· https://vieillemarine.pagesperso-orange.fr/

Revenir au sommaire

[1] Source : Anthiaume – "Evolution et enseignement de la science nautique".

[3] Source : Archives de la Marine, citées par Anthiaume.

[4] Cité par A. J. Turner dans Time Museum – Time Measuring Instruments.

[5] Voir D'Hollander – Sciences géographiques dans l'antiquité.

LE CERCLE UNIVERSEL DE NAVIGATION DE BOISSAYE DU BOCAGE Un abaque de marine normand en usage à la fin du XVIIe siècle