Les principes de
l’astrolabe
« Prendre » les étoiles
« Astrolabe » est un mot d’origine grecque que l’on peut littéralement traduire par « preneur d’étoiles ». En grec, astron signifie étoile et labê dérive du verbe lambanein qui signifie prendre.
Ce que l’astrolabe « prend » aux étoiles, c’est
leur angle d’altitude (ou « hauteur ») au-dessus de l’horizon.
L’angle d’altitude est une des deux coordonnées locales (l’autre est l’angle d’azimut)
qui permet de localiser les étoiles depuis l’altitude 0°, correspondant au
niveau de l’horizon, jusqu’à l’altitude 90°, correspondant à la verticale de l’observateur
c’est-à-dire au point du ciel situé au-dessus de sa tête, que l’on nomme le « zénith ».
En imaginant une grande demi-sphère centrée sur l’observateur, la « sphère
locale » comme indiquée sur la figure 1, on peut représenter les
cercles d’altitude, par exemple tous les dix degrés.

Figure 1: cercles d’altitude, depuis l’horizon jusqu’au zénith, sur la sphère céleste locale.
Pour mesurer l’angle d’altitude d’une étoile, on utilise le dos de l’astrolabe, tenu verticalement. Une règle de visée, l’alidade (un mot arabe) tourne le long d’un arc de cercle gradué de 0° à 90°.
Pour « prendre une étoile », on tient l’astrolabe par son anneau de suspension et on ajuste l’alidade pour aligner l’étoile dans les deux trous (les pinnules) de visée (voir figure 2). On lit alors l’angle d’altitude grâce au rapporteur de 90 degrés gradué sur le bord extérieur de l’astrolabe.
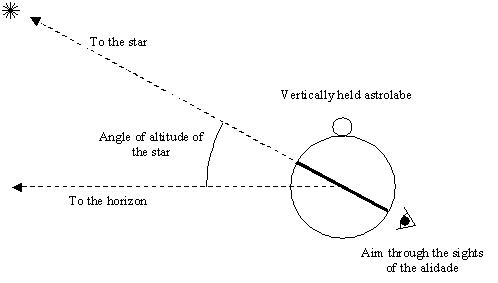
Figure 2: mesure avec un astrolabe
de l’altitude d’une étoile.
(l’astrolabe est tenu verticalement et
on vise l’étoile à travers les pinnules de l’alidade
pour obtenir l’angle d’altitude de l’étoile.)
Une fois la mesure de l’angle d’altitude effectuée, on doit reporter le résultat sur la face astronomique de l’astrolabe, de sorte à placer le ciel dans sa position apparente au moment de l’observation.
C’est la représentation géométrique du ciel et de ses mouvements apparents, reproduite sur l’astrolabe, qui permet l’exploitation de la mesure qui vient d’être effectuée.
Un joyau de la géométrie grecque
Au court du temps, pour un observateur situé à un point fixé de la Terre, les étoiles semblent tourner autour du pôle céleste. C’est assez évident la nuit, lorsque l’on voit les constellations tourner approximativement autour de l’étoile polaire (voir la figure 3), mais aussi le jour, où le Soleil semble se déplacer de façon analogue.
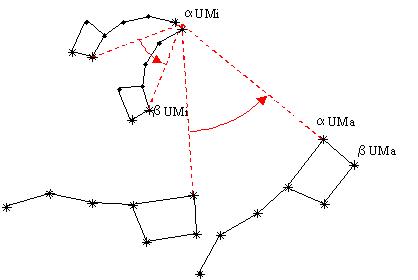
Figure 3: rotation apparente des deux Ourses la nuit, autour du pôle Nord céleste.
On peut alors, comme les Grecs, imaginer que les étoiles sont fixées sur une sphère, nommée « sphère céleste », centrée sur la Terre et en rotation autour de celle-ci. Avec ce modèle, le mouvement apparent des étoiles et du Soleil est simulé en utilisant deux sphères, la sphère locale immobile, où apparaissent entre autres les cercles d’altitude, et la sphère céleste, en rotation selon l’axe des pôles, où apparaissent les étoiles et le Soleil (voir la figure 4).
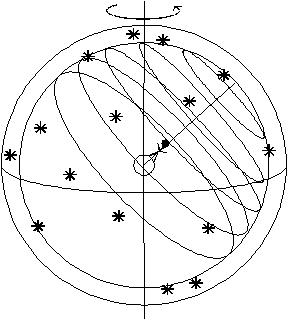
Figure 4: la sphère locale fixe entourée de la sphère céleste en rotation.
La sphère armillaire (armilla signifie anneau en latin) est une représentation concrète de ces deux sphères (voir la figure 5). La sphère locale fixe comprend, entre autres, le cercle horizon et le cercle du méridien local, où se trouve le Soleil à la mi-journée. Alors que le cercle de l’écliptique, indiquant les positions annuelles du Soleil, se trouve sur la sphère céleste mobile.

Figure 5: sphère armillaire.
La face astronomique de l’astrolabe correspond à la projection de ces deux sphères. De cette façon, l’astrolabe permettra de simuler « à plat » le mouvement apparent des étoiles. Ce sera plus pratique, pour voyager, que de fragiles sphères, et c’est aussi moins cher à fabriquer.
Le principe de cet « aplatissement » est celui de la projection stéréographique (« stéréographique » signifie en volume).
C’est une (assez) simple projection « visuelle ». Imaginez-vous situé au pôle céleste Sud (voir sur la figure 6). De cet endroit, regardez les étoiles situées en A et B sur la sphère céleste. Les projections A’ et B’ de ces étoiles sur le plan de l’équateur seront situées aux points où les rayons visuels rencontrent le plan de l’équateur céleste.
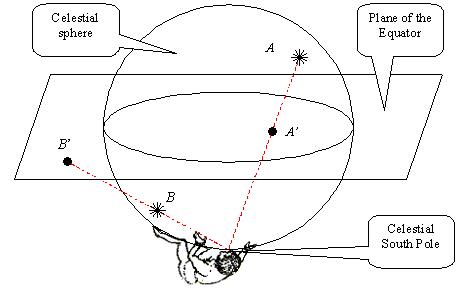
Figure 6: projection stéréographique
sur le plan de l’équateur.
On remarque que plus l’étoile est proche du pôle Sud, plus sa projection s’éloigne du centre du cercle de l’équateur. On ne peut pas « aplatir » une sphère sans déformation et l’astrolabe planisphérique ne sera pas capable de représenter le ciel entièrement. On convient de limiter l’astrolabe au tropique du Capricorne céleste (voir la figure 7).
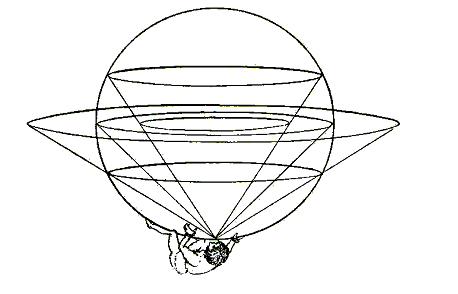
Figure 7: projection stéréographique de l’équateur et des tropiques (célestes).
Une des plus importantes propriétés de cette projection est de représenter les cercles tracés sur la sphère par des cercles du plan (ou des droites lorsque le cercle de la sphère passe par le pôle Sud). Cette propriété mathématique est d’un grand secours pour la construction de l’astrolabe car il est simple de tracer un cercle (plutôt qu’une ellipse ou une autre courbe).
Le principe de la projection stéréographique a été étudié par Apollonius de Perge, un mathématicien du troisième siècle avant notre ère. Il fut ensuite appliqué à l’astronomie par Hipparque vers 150 avant notre ère avant d’être utilisé par Ptolémée, vers 150 de notre ère, dans une sorte de planisphère céleste rotatoire, ancêtre de l’astrolabe.
Il est facile de voir (avec les connaissances mathématiques de la classe de troisième) que la projection A’ du point A, situé dans l’hémisphère céleste Nord, est donnée par la formule (voir la figure 8) :
![]()
(où R est le rayon de la sphère et x l’angle A’OA , « déclinaison » de A).
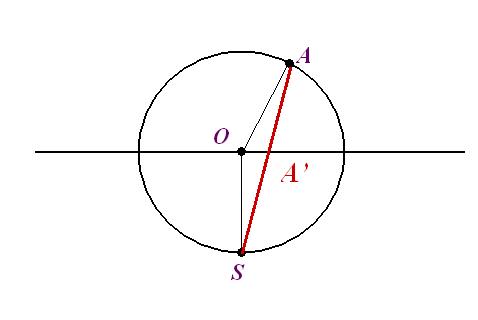
Figure 8: projection du point A situé
dans l’hémisphère Nord.
Par ailleurs, on utilise la formule suivante pour trouver la projection B’ d’un point B situé dans l’hémisphère Sud :
![]()
(où R est le rayon de la sphère et y l’angle B’OB , « déclinaison » de B).
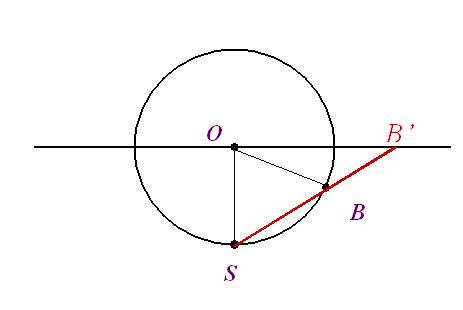
Figure 9: projection d’un point B situé dans l’hémisphère Sud.
La projection des deux sphères nous fournit les deux pièces nécessaires à la constitution de la face astronomique de l’astrolabe (voir la figure 10) :
· Le tympan correspond à la sphère locale et est tracé pour une latitude d’observation spécifique. Le cercle représentant l’horizon et les arcs d’altitude, jusqu’au zénith, sont figurés sur le tympan.
· L’araignée (nommée ainsi pour son réseau en forme de toile) correspond à la sphère céleste. Elle représente une carte céleste en rotation autour du pôle Nord céleste (le centre de l’araignée correspond approximativement à l’étoile polaire).
Au cours de l’année, les étoiles « fixes » ne se déplacent pas les unes par rapport aux autres dans le ciel nocturne (le mouvement est global). Les pointes de l’araignée correspondent aux étoiles de cette carte céleste. Le Soleil en revanche semble se déplacer au court de l’année sur le ciel étoilé, sa position par rapport aux étoiles est indiquée sur l’araignée par la date du calendrier.
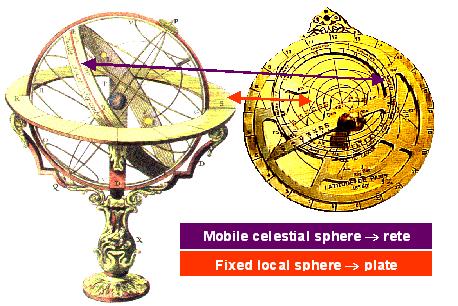
Figure 10: les deux parties de la face astronomique en 2 dimensions de l’astrolabe
proviennent de la sphère armillaire en 3 dimensions.
Sphère céleste mobile --> Araignée
Sphère locale fixe --> Tympan.