UN ASTROLABE
QUADRANT
OTTOMAN
L'affichage des expressions écrites en arabe
nécessite les polices Urdu et Malik Lt BT. Il est possible de les télécharger
sur Internet en faisant une recherche à partir de Google par exemple. On peut aussi
s'en passer en ignorant les symboles étranges qui leur seront substitués…
Description de l'instrument
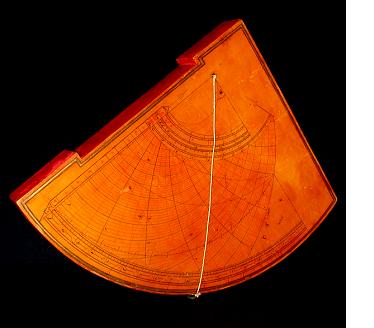
En bois laqué, mesurant 17,4cm ´ 15cm, ce quadrant est marqué sur la face avant (1ère image) comme un astrolabe-quadrant, dit "de Profatius", liant le temps à la hauteur du Soleil, et, au dos (2ème image), comme un "quadrant des sinus", à usage trigonométrique.
Les inscriptions et les lignes sont inscrites en noir, rouge et or, sur fond ocre. Les bords sont cerclés d’un liserait or, les tranches sont rouges. Sur un bord, une partie en creux a été ménagée de façon à constituer le viseur.
Le quadrant est traversé par un fil. Le plomb manque, ainsi que la perle mobile.
Les écritures, rouges ou noirs, les motifs dorés, sont d'une grande finesse, qui rappelle les enluminures ottomanes. L'outil principal pour ce faire est le pinceau, en voici la description, donnée dans un ouvrage sur les arts décoratifs turcs[1] :
"Pour tracer les lignes en or ou en couleur, d'une finesse extrême, on emploie des pinceaux spécialement préparés, à un seul poil. Ces pinceaux sont faits de jeunes poils, provenant de la nuque d'un chat de trois mois. Plusieurs de ces poils sont réunis ensemble de façon à laisser le poil le plus long vers le bout et attaché du côté opposé par un fil de soie. Ces poils réunis sont passés ensuite dans le creux d'une plume de colombe. La plume de poule n'étant pas droite, comme celle-ci, ne convient pas à tracer et peindre sans déviation. Le pinceau ainsi préparé est passé ensuite sur une tige en bois et est prêt à servir. Si le poil de bout n'est pas assez net et aigu, on l'approche légèrement d'une tête d'allumette à peine éteinte pour brûler les aspérités et faire disparaître ainsi les irrégularités."
Sur la face avant, le quadrant est signé à l'apex, çyBU (Khaky).
En
bas de l'échelle des lignes de hauteurs (al-muqantarāt) apparaît,
en chiffres arabes orientaux, la date de construction de l'instrument 1 2 8 0 soit 1280 de l'Hégire.
Pour retrouver l'année correspondante du calendrier grégorien, un petit calcul est nécessaire. Le calendrier lunaire musulman a été élaboré par le 2ème calife (Omar Ier). Son origine est fixée au 16 juillet 622 A.D., date théorique de la fuite du Prophète à Médine. Disposer d'un calendrier était une affaire de prestige et d'affirmation. Selon le calife Omar, le choix de l'émigration de Mahomet est fait parce que "l'émigration a établi la distinction entre la vérité et l'erreur."
Sur un cycle de 30 ans, le calendrier musulman compte 11 années de 355 jours et 19 années de 354 jours, soit une année moyenne de 354,36667 jours.
Entre le début de l'ère de l'Hégire et la fin de l'année 1280 se sont donc écoulés 1281´354,36667 » 453 944 jours. En divisant par 365,25 on trouve environ 1242,8 années solaires.
En ajoutant 622, on obtient, pour la fin de l'année 1280 A.H., 1864,8 A.D. .
Ainsi, 1280 A.H. (Anno Hijrae) correspond à 1863/1864 A.D. (ab incartione Domini).
Tous les autres nombres apparaissant sur le quadrant sont en notation alphabétique Abjad.
Il en est ainsi de la latitude pour laquelle sont effectués les tracés du tympan astrolabique. Celle-ci est indiquée en dessous de la ligne d'horizon : hZk ( 'arḍ) en lettres noires, 43°30' , en lettres rouges.
Le nombre 40 correspond à la lettre mim w (m) ,le nombre 3 à la lettre jīm Q (j), le point n'est pas indiqué, et le nombre 30 correspond à lām {. (l).
On peut vérifier que cette latitude correspond effectivement, sur les tracés du quadrant, à la hauteur du pôle au dessus de l'horizon.
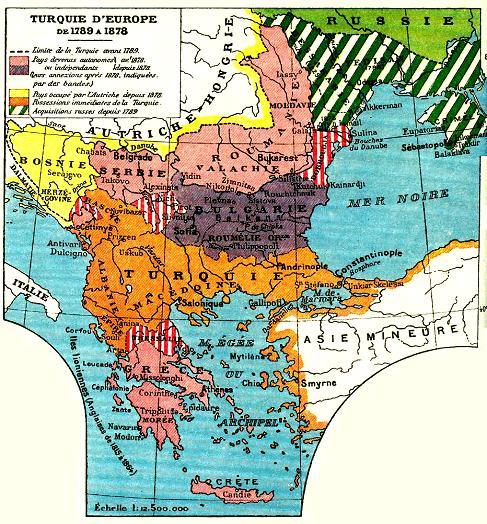
Il peut s'agir de la Bosnie : la ville de Sarajevo est à 43,8° de latitude nord, celle de Mostar à 43,3°. L'instrument était sans doute destiné à une utilisation dans cette région. Jusqu'en 1878 en effet, la Bosnie fait partie de l'empire ottoman.
Historique des quadrants
· Le premier type de quadrant (quart de cercle) est le quadrant d'altitude, connu dès l'antiquité. Gradué en 90 degrés, muni d'un fil à plomb et d'un système de visée, il permet la mesure de la hauteur des astres : le fil à plomb donne, en même temps que l'on effectue la visée, l'angle de hauteur par rapport à l'horizontale.
Ce quadrant a été ensuite adapté aux besoins de la trigonométrie et de la mesure du temps.
· Le quadrant des sinus (al-rub' al-mukhayyab) a été développé par les arabes à Bagdad au IXème siècle, et est resté populaire pendant 1000 ans (on le retrouve au dos de notre quadrant du XIXème). Il ressemble à du papier millimétré et fonctionne avec une corde munie d'une perle mobile, permettant d'effectuer des calculs trigonométriques.
· Le quadrant horaire a sans doute été
développé à la même époque. Ses lignes permettent de traduire la hauteur du
Soleil en heures de la journée. Il s'agit le plus souvent des heures inégales,
ou saisonnières, correspondant à la division en 12 de la durée comprise entre
le lever et le coucher du Soleil. On trouve un tel quadrant en haut de la face
astrolabe de notre instrument. Ce quadrant, lorsqu'il est à curseur fixe,
correspond à une latitude donnée, mais, muni d'un curseur mobile, il est
utilisable à toutes les latitudes. Un texte du IXème siècle,
découvert au Caire vers 1980, décrit le quadrant horaire avec curseur fixe et
mobile, alors qu'on pensait que ce dernier était une invention du Moyen-âge
européen[2].
Ces quadrants ont été très populaires, au point que le terme de cadran vint à
désigner des instruments de mesure du temps n'ayant plus la forme d'un quart de
cercle (voire même le cadran de la montre).
· L'origine de l'astrolabe-quadrant est plus mystérieuse. L'idée peut sembler simple. Il s'agit d'utiliser la symétrie du tympan de l'astrolabe par rapport à la droite méridienne et de remplacer l'araignée par une corde où une perle mobile occupe la position du Soleil. L'instrument est alors facile à fabriquer, très peu coûteux et, substituant un quart de disque au disque entier, est relativement plus grand et donc, a priori, plus précis.
En 1288, l'astronome juif Ibn-Tibbon dit Profatius, établi à Montpellier, écrit en hébreu un traité décrivant un astrolabe-quadrant de son invention (ce traité sera traduit en latin en 1290). Après suppression des arcs de hauteur et d'azimut du tympan de l'astrolabe, et l'ajout de plusieurs lignes d'horizon, pour des latitudes différentes, le tympan, plié en quatre, donne naissance à ce nouveau type de quadrant. Très peu d'exemplaires de quadrants de ce type sont parvenus jusqu'à nous et son utilisation était assez difficile puisqu'il ne fournissait pas mécaniquement l'heure, mais qu'un calcul trigonométrique assez sophistiqué était nécessaire pour l'obtenir.
Dans le monde musulman se développe un astrolabe-quadrant désigné par "quadrant des arcs de hauteur" (rub' al-muquantarāt) dont on a pu penser qu'il était dérivé du quadrant de Profatius.
Le quadrant ottoman que nous étudions est de ce type. On constate cependant que le quadrant de Profatius ne comporte justement pas les arcs de hauteurs, almucantarats.
Le quadrant almucantar est lui beaucoup plus proche de l'astrolabe et permet la lecture directe de l'heure de jour. En revanche, son tracé, et son utilisation, est limité à une latitude donnée.
D'après D. King, "un manuscrit sur l'utilisation du quadrant almucantar, d'origine égyptienne et datable du XIIème siècle, a été découvert récemment [article de 1981] à Istanbul et son auteur ne s'en réclame pas l'inventeur".
A partir du XVIe siècle, les astrolabes quadrant ont tendance à remplacer les astrolabes dans le monde musulman (sauf en Perse et en Inde).
Ci-dessous, un exemple typique de la production maghrébine du XVIIe siècle.
Au XVIe siècle, on trouve certains "embellissements" au cadran de Profatius, dans les traités d'Apian et de Finé.
Au XVIIe siècle, apparaissent en Angleterre d'autres types d'astrolabes-quadrant. Il s'agit d'abord du quadrant de Gunter. En 1618, Edmund Gunter montre à Henry Briggs et William Oughtred, au Gresham College, un nouveau quadrant, qu'il décrira dans son ouvrage, publié en 1623. Il s'agit d'un quadrant plus simple à utiliser que celui de Profatius, qui connu un certain succès, en particulier en navigation. Cinq étoiles étaient couramment indiquées et permettaient de connaître l'heure la nuit : Markab (a Pegasi), Aldebaran, Regulus, Arcturus et Altaïr.
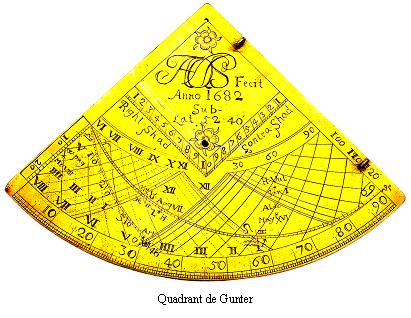
En 1658, John Collins donne d'autres formes au quadrant de Gunter et Henry Sutton construit des quadrants similaires à ceux décrits par Collins.
La mesure du temps dans la Turquie ottomane
La tradition astronomique ottomane puise à deux sources : la première d'Asie centrale (l'observatoire de Samarkand date du XVe siècle), la seconde d'Egypte et de Syrie, à Damas et au Caire au XIVe siècle.
La miniature ci-contre représente ainsi des astronomes au travail dans l'observatoire de Taqī ad-Dīn à Istanbul (quartier Galata) vers 985 AH, 1578 AD.
La préoccupation principale était la mesure du temps, 'ilm al-mīqāt, en particulier pour la détermination des heures des cinq prières (voir plus loin).
Au XIIe siècle, en Egypte, apparaît le muwaqqit, un astronome professionnel attaché à une institution religieuse et dont la tâche principale est la réglementation des heures des prières.
A l'époque ottomane, des bâtiments, les muwaqqithanes, sont adjoints aux principales mosquées, et utilisés par les muwaqqits.
Selon D. King, "aux époques mamelouke et ottomane tardives, les muwaqqits compilèrent de nombreux traités concernant les formules de calcul du temps, et les procédures pour calculer l'heure du jour ou de la nuit, ou les heures de prière, au moyen d'un quadrant des almucantars ou d'un quadrant des sinus."
Il nous est ainsi permis d'imaginer que l'astrolabe-quadrant que nous étudions a appartenu à l'un de ces muwaqqits du XIXe siècle, dans la région de Sarajevo.
Les tracés de la face "astrolabe"
Le quadrant de hauteur
Le principe du quadrant de hauteur est très simple.
On tient le quadrant verticalement et on l'incline de sorte que l'ombre du premier bord de l'encoche du viseur recouvre le second bord (le viseur à encoche ottoman remplace le système à pinnule).
Le fil à plomb marque alors, sur le bord arrondi du quadrant, un angle h égal à celui du Soleil par rapport à l'horizon.
L'arc de hauteur du quadrant est marqué d'une double échelle en degrés, divisée de 0° à 90° dans les deux directions, numérotée tous les 5°, subdivisée tous les degrés.
Les principales lignes du tympan
On reconnaît (voir au préalable l'article "Astrolabe" de ce site) un quart de tympan, calculé ici pour la latitude de 43°30' Nord, et tracé entre les tropiques du Cancer et du Capricorne. En fait le quadrant figure même la moitié Est du ciel au dessus de l'horizon.
Les arcs de hauteur (almucantarats) sont tracés, à partir de l'horizon, tous les degrés simples en rouge et tous les 5 degrés en noir. Ils sont gradués en rouge, de 25° à 70°, tous les 5°, le long du méridien (voir figure page suivante).
Les arcs d'égal azimut sont tracés en rouge tous les 5 degrés et en noir tous les 15 degrés. Ils sont gradués en noir tous les 15 degrés, d'abord le long de l'horizon, puis le long du tropique du Capricorne. L'arc Est-Ouest se distingue par des petits points dorés à chaque arc de hauteur rencontré.
L'horizon et l'équateur sont indiqués en noir.
L'écliptique est tracé en deux arcs noirs. La partie notée "arc 2" sur la page précédente est obtenue par symétrie par rapport à la droite Est-Nord de la portion de l'écliptique située sous l'horizon. En positionnant la perle, coulissant sur le fil, à la position du Soleil sur l'écliptique, on remplacera l'écliptique de l'araignée de l'astrolabe en faisant tourner le fil tendu. Ainsi, ce qui compte est la distance du point de l'écliptique, correspondant à la date du jour, au pôle ou est fixé le fil. La position particulière de l'écliptique, fixe sur le quadrant, et le relèvement par symétrie de sa partie inférieure, sont donc sans incidence pour l'utilisation que l'on en fait.
Le premier arc de l'écliptique, sous l'équateur, est gradué tous les degrés, avec un trait plus long marqué de deux points dorés tous les 5 degrés. La séparation entre chaque signe du zodiaque est marquée d'un long trait prolongé par deux flèches formées de 7 points dorés. Le second arc de l'écliptique n'est gradué qu'à chaque séparation de signe, mais il est possible, avec la corde, d'utiliser les graduations précédentes.
Un exemple d'utilisation : détermination de la
hauteur méridienne hm du Soleil
Un jour donné, la hauteur méridienne hm du Soleil, est l'angle de hauteur maximum qu'il fait, dans la journée, avec l'horizon. Cette hauteur maximale est obtenu quand le Soleil passe au méridien, à midi. On a hm = 90° – j – d où j = 43°30' est la latitude et d est la déclinaison du Soleil.
On tend le fil et on déplace la perle de façon à l'amener à la position du Soleil sur l'écliptique à la date donnée.
En gardant la perle en place, on tourne le fil tendu, pour l'amener sur le méridien. On lit la hauteur méridienne hm du jour, sur l'arc de hauteur correspondant. On peut s'aider de la graduation des hauteurs indiquée en rouge le long du méridien.
Le quadrant des heures inégales
Le tympan astrolabique est surmonté d'un petit quadrant des heures inégales. Rappelons que ces heures, très utilisées dans le monde antique, au Moyen-Age, au Japon encore au XIXe et ici en Turquie, consistent à diviser le jour en 12 heures depuis le lever jusqu'au coucher du Soleil.
L'indication "heures saisonnières" figure à l'extrémité de l'échelle du quadrant horaire :
[sā'āt
al-] zamāniyā ¨xB}g .
Utilisation
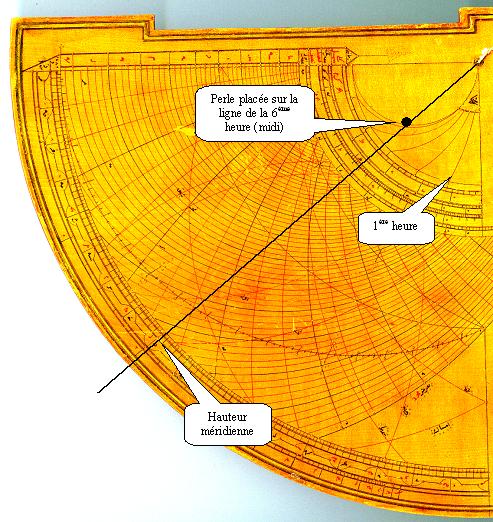
On règle la perle de sorte que la hauteur méridienne corresponde à la 6ème heure : on place le fil sur la graduation noire de l'arc des mesures de hauteur, correspondant à la hauteur méridienne du jour. On glisse la perle de sorte qu'elle se situe sur la ligne de la 6ème heure du quadrant des heures inégales.
On prend le Soleil à travers le viseur. La perle du fil à plomb indique alors l'heure inégale sur le quadrant de hauteur.
Les échelles situées sous le quadrant des heures
inégales
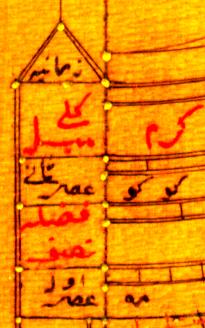
Sous le quadrant des heures inégales, apparaissent 4 échelles, sur des quarts de cercle centrés sur le pôle. Elles s'utilisent avec le fil et correspondent à :
· la déclinaison du Soleil,
· la hauteur du Soleil lors de la 2ème prière de l'après-midi,
· l'arc semi-diurne intervenant dans l'écart entre les heures égales et inégales,
· la hauteur du Soleil lors de la 1ère prière de l'après-midi,
|
Déclinaison kullī mayl |§} ¨{y |
|
2ème prière de l'après-midi thānī 'aşr Zek ¨YBM |
|
Arc semi-diurne fađla nişf seY |gs |
|
1ère prière de l'après-midi āwal 'aşr Zek |zA |
La première échelle indique la déclinaison d du Soleil lorsque l'on aligne le fil avec la position de celui-ci sur l'écliptique. Elle est divisée de 0° à 23°30' tous les degrés et numérotée tous les 5 degrés :
Hā ه pour 5 ; Yā ¨ pour 10 et Kāf y pour 20.
Les échelles 2 et 4 indiquent la hauteur du Soleil pour la prière 'aşr en fonction de la hauteur méridienne hm du Soleil. Soit que l'on fasse deux prières (?) ou, plus vraisemblablement, pour indiquer le début et la fin de l'intervalle de temps où l'on peut faire cette prière. On aligne le fil sur la valeur de l'échelle des hauteurs (au bord circulaire du quadrant) correspondant à la hauteur méridienne du jour. Les graduations sous le fil correspondent alors, pour la 2ème échelle, à la hauteur du Soleil pour la 2ème 'aşr , et, pour la 4ème échelle, à la hauteur du Soleil pour la 1ère 'aşr .
Voici deux exemples de résultats, obtenus avec ces échelles. Ces résultats peuvent encore être obtenus de deux autres façons en utilisant ce quadrant. Soit avec les courbes situées sur le tympan, soit avec l'abaque situé, au dos, sur le quadrant des sinus. Cela devait être très important !
|
|
hm |
42° |
55° |
|
|
|
1ère 'aşr |
25° |
30° |
|
|
|
2ème 'aşr |
» 18° |
20° |
|
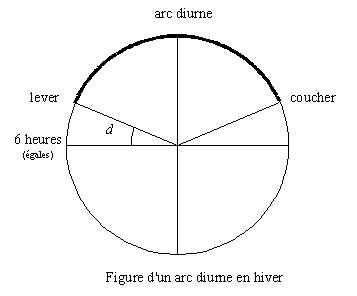
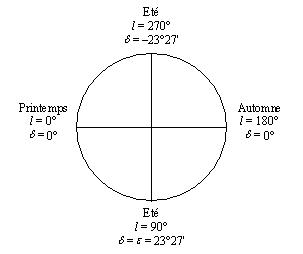
La seconde échelle fournit l'arc semi-diurne d , valeur angulaire, comptée positivement en été, négativement en hiver, correspondant à l'écart entre la 6ème heure égale et le lever du Soleil, 0ème heure inégale.
La
valeur de l'arc diurne est ainsi, en degrés, 180° + 2d , où d est négatif lorsque la durée du jour est inférieure à celle de la
nuit (dessin ci-contre).
Une formule donne la valeur de d en fonction de la déclinaison d du Soleil et de la latitude j du lieu :
sin d = tan d ´ tan j .
L'échelle du quadrant indique l'arc semi-diurne d lorsque le fil est aligné sur la position du Soleil sur l'écliptique.
La connaissance de d permet la conversion entre heures égales et heures inégales : une heure égale correspond à 15° et une heure inégale à (15 + d/6)°.
De plus, l'importance de cette quantité tenait aussi au fait que les ottomans, au XIXe siècle, avaient l'habitude de compter les heures (égales) avec la convention que le coucher du Soleil marque 12 heures (ou 0 heure) sur l'horloge. "Cette convention, inspirée par le fait que le jour musulman commence au coucher du Soleil (parce que le calendrier est lunaire et que les mois commencent avec la visibilité du [premier] croissant peu après le coucher du Soleil), a l'inconvénient que les horloges marquant les "heures turques" doivent être rectifiées de quelques minutes au bout de quelques jours."[3]
L'échelle des cotangentes
En dessous de l'arc de mesure des hauteurs, se trouve une échelle des cotangentes. Les cotangentes sont données sur une base 12 (duodécimale) : on y lit cotan a ´ 12 , ainsi en face de l'angle de 45°, on lit la valeur 12 sur l'échelle des cotangentes. L'échelle est graduée toutes les unités et numérotée tous les 5, en rouge.
Parce qu'elle est duodécimale, cette échelle est désignée sous le nom d'échelle en pouces (12 pouces égalent un pied ! ). Elle correspond à l'ombre droite d'un gnomon de 12 pouces. La longueur r de l'ombre "droite" est donnée par lecture de l'échelle des cotangentes en pouces et peut se faire simultanément avec la visée du Soleil.
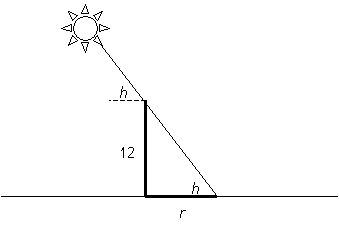
On a tan h = 12/r donc r = 12 ´ cotan h .
On vérifie par exemple que : cotan 67°30' ´ 12 » 4,97 » 5
et cotan 15° ´ 12 » 44,78 » 45.
La construction de cette échelle à partir d'un carré des ombres de côté 12 est indiquée par la figure ci-contre[4]. On gradue régulièrement l'axe des ombres droites, en le prolongeant, puis les rayons obtenus en alignant avec le centre permettent la graduation des cotangentes sur le bord du quadrant.
Alors que l'échelle des ombres droites du carré des ombres n'indique que les cotangentes des angles de hauteurs supérieurs à 45°, l'échelle circulaire permet, pour notre quadrant, de descendre jusqu'à 11°30'.
Les lignes des prières
Les définitions des heures de 5 prières (şalāt) indiquées, de façon peu précise, dans le Coran, ont été mises en forme canonique au VIIe siècle. Les deux prières de jour sont définies par la longueur des ombres, celles de nuit par la position du Soleil par rapport à l'horizon local. Elles dépendent ainsi de la latitude et du moment de l'année. De plus, la prière est interdite à certaines heures, en particulier aux instants du lever, de la culmination et du coucher du Soleil. Il s'agissait de distinguer les musulmans de certaines religions concurrentes, en particulier des Sabéens, et surtout des zoroastriens, adorateurs du Soleil. Dans le "Traité exhaustif des ombres", le grand astronome Al-Bīrūnī (971 – 1038) s'exprime ainsi[5] : "Prier aux trois instants mentionnés ci-dessus [lever, culmination, coucher] est interdit pour nous distinguer [de ces sectes]. On dit que le Soleil se lève entre les cornes de Satan, pour dire que ses associés vénèrent le Soleil à cet instant."
Les cinq prières, et leur "définition" dans le Coran :
|
1 |
2 |
3 |
4 |
5 |
|
Coucher |
Tombée de la nuit |
Aube |
"Midi" |
Après-midi |
|
maghrib JZp} samar
? Z}a |
'ishā' YBck shafaq
? xtc |
fajr ZOs |
żuhr Zﻬj |
'aşr Zek |
|
Extrémité de la lumière du jour (crépuscule) |
Première partie de la nuit |
Extrémité de la nuit |
Déclin du Soleil |
Avant le coucher du Soleil |
Le đuħā est une prière supplémentaire en usage dans certaines communautés.
C'est Al-Khwārismī qui, pour la latitude de Bagdad au début du IXe siècle, donna les premières tables (zīj) connues pour régler les heures des prières de jour. Cependant, Al-Khwārismī hésite encore entre plusieurs définitions du żuhr pour l'associer avec la 6ème ou la 7ème heure inégale[6]. A partir du IXe siècle, on trouve des descriptions indiquant comment trouver les heures des prières avec un instrument tel que l'astrolabe. Au XIe siècle, Al-Bīrūnī , dans le "Traité exhaustif des ombres" précise les règles définies précédemment.
En fait, avant le XIIIe siècle, la fixation des heures de prières est, dans la pratique, le travail du muezzin (mu'hadhdhin) qui ne possède que des rudiments d'astronomie populaire, se fondant sur des moyens mnémotechniques, et n'utilisant ni table ni instrument. La tendance scientifique a, de plus, longtemps été combattue. Al-Aşbaħī (Yémen, XIIIe siècle) déclarait par exemple[7] :
"Les heures de prière ne sont pas à rechercher avec les degrés marqués sur un astrolabe et pas par des calculs usant de la science des astronomes, elles sont à trouver uniquement par l'observation… Les astronomes tirent leur connaissance d'Euclide et de Sindhind, et d'Aristote et autres philosophes, tous étaient infidèles."
C'est en Egypte que l'on trouve mention, pour la première fois, d'astronomes spécialisés dans la trigonométrie sphérique et la mesure du temps, les muwaqqit, associés à une institution religieuse pour les heures des prières, et les mīqātī, non nécessairement attachés à une institution religieuse. Abū 'Ali al-Marrākushi est l'un de ces mīqātī, installé au Caire à la fin du XIIIe siècle. Son "Traité des instruments astronomiques des Arabes", étudié au XIXe par les Sédillot, père et fils, traite de la mesure astronomique du temps.
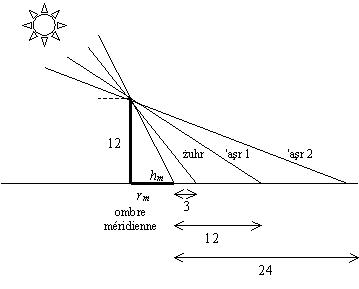
On constate que les lignes tracées pour la prière 'aşr sur notre quadrant ottoman, sont conformes à la règle énoncée par Al-Bīrūnī au IXe siècle dans son "Traité exhaustif des ombres". Elles sont résumées sur le dessin ci-dessous, pour un gnomon de 12 pouces.
|
hauteur méridienne hm |
ombre méridienne
|
'aşr 1
|
'aşr 1 hauteur lue sur le
quadrant |
'aşr 2
|
'aşr 2 hauteur lue sur le
quadrant |
|
42° |
13,33 |
25,35° |
» 25° |
17,82° |
» 18° |
|
55° |
8,40 |
30,47° |
» 30° |
20,32° |
» 20° |
Les lignes des prières, figurant sur le quadrant ottoman, sont les suivantes :
La prière đuhā, du matin, appartient bien au cadran 1 du tympan de l'astrolabe. Les lignes pour la prière de 'aşr appartiennent au cadran 2 de l'astrolabe (après-midi) mais sont ramenées sur le quadrant par symétrie par rapport au méridien. L'utilisation de ces trois lignes de prière est très simple. La perle étant placée sur le fil selon la position du Soleil sur l'écliptique, il suffit de prendre le Soleil dans le viseur en tenant le quadrant verticalement. Lorsque la perle est sur la ligne, on appelle à la prière (la hauteur du Soleil correspond).
Pour les lignes des prières du crépuscule et de la
nuit, situées a priori dans le cadran 3, elles sont ramenées sur le cadran 1
par symétrie par rapport au pôle. Pour utiliser ces lignes, au lieu de placer
la perle sur le point solaire, on doit la placer sur le point anti-solaire,
situé sur le signe zodiacal opposé sur l'écliptique. On n'utilise pas la
lumière du Soleil (il est
couché ! ), mais en plaçant la perle sur la ligne correspondante, le fil
indique sur l'échelle angulaire extérieure, l'heure égale à laquelle se fait la
prière.
Pour la ligne de la prière fajr, ramenée du cadran 4 au 1 par symétrie axiale, on utilise également le point anti-solaire, dont l'image à l'instant de cette prière, se trouverait dans le cadran 2.
Deux courbes supplémentaires indiquent le début du jeûne pour le mois de Ramadan (marquée courbe du début du jeûne khaţ imsāk zBa}A iU ) et la prière pour les deux fêtes principales (marquée courbe de l'aïd khaţ 'īd Xk iU ).
Les tracés de la face trigonométrique
Le dos de l'astrolabe-quadrant ottoman est tracé selon un quadrant des sinus. Il permet notamment d'obtenir directement les fonctions circulaires de la hauteur h de l'astre visé.
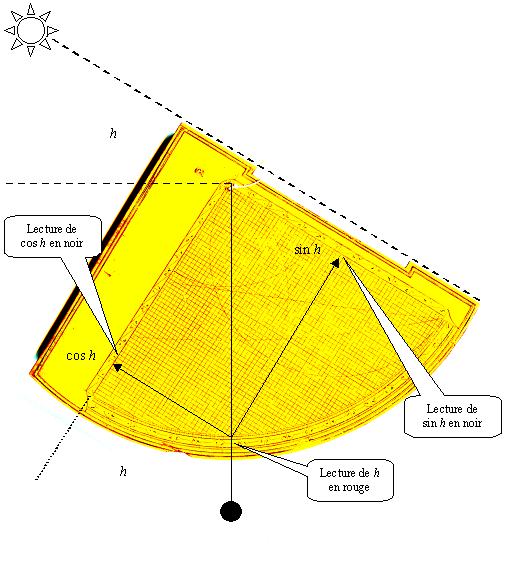
Quadrillage des sinus et cosinus
L'arc des hauteurs est marqué d'une double graduation de 0° à 90° dans les deux directions (en rouge l'angle de hauteur h et en noir son complément). L'échelle est subdivisée tous les demi-degrés et numérotée tous le 5°.
Les axes des cosinus et sinus sont numérotés en système sexagésimal, de 0 à 60 ( s b indique 60 en notation abjad), toutes les 5 unités, dans les deux sens : en noir la valeur du cosinus (ou du sinus), en rouge celle de son complément à 60 (le complément du cosinus est désigné par sinus verse au Moyen-Age). Le quadrillage correspond à l'unité.
Arcs des sinus (ou cosinus)
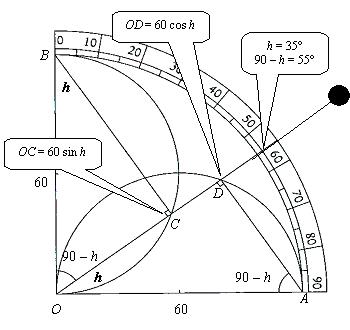
Les deux arcs de cercle ayant pour diamètre les segments OA = 60 et OB = 60 servent à la détermination des sinus et cosinus d'un angle h compris entre 0° et 90°, à l'aide d'une perle glissant sur le fil. C'est une autre façon de procéder, n'utilisant pas le quadrillage.
Sur la figure, on a :
Ainsi, les longueurs OC et OD correspondent respectivement, en sexagésimal, au sinus et au cosinus de l'angle h.
Il suffit alors de faire glisser la perle, de la positionner sur C ou sur D, puis de ramener le fil sur [OA] pour y lire la valeur sexagésimale du sinus ou du cosinus.
On peut bien sûr fonctionner à l'envers, partir d'une valeur sur [OA] et trouver l'angle dont le sinus ou le cosinus correspond à cette valeur.
Arc de l'obliquité de l'écliptique
Un quart de cercle dont le rayon correspond au sinus de l'obliquité de l'écliptique permet d'obtenir la déclinaison d du Soleil en fonction de sa longitude l céleste (angle compté sur l'écliptique à partir du point g correspondant à l'équinoxe de printemps).
La formule permettant ce calcul est la suivante :
d = Arcsin( sin e ´
sin l ) .
La valeur prise pour l'obliquité de l'écliptique est ici e = 23°30'. On constate que la valeur du rayon de l'arc de l'obliquité est bien
sin e ´ 60 » 23,9
sur la graduation sexagésimale du segment [OA].
On place le fil de façon à former un angle l correspondant à la longitude céleste du Soleil. Par exemple l = 55°. Le fil coupe l'arc de l'obliquité de l'écliptique au niveau du point C. Puisque OC = sin e , la projection D de C sur [OB] donne OD = sin e ´ sin l.
Il suffit alors d'aller chercher l'angle d = Arcsin( sin e ´ sin l ) correspondant à cette valeur du sinus.
Cela peut par exemple se faire en positionnant la
perle sur la longueur OD puis en plaçant le fil de sorte que la perle
soit sur l'arc des sinus.
On lit, pour l'exemple l = 55°, d »
19°.
Lignes pour la prière 'aşr
Deux lignes tracées en rouge permettent de retrouver la hauteur h du Soleil au moment de la prière 'aşr en fonction de la hauteur méridienne hm du Soleil.
Prenons par exemple une hauteur méridienne hm de 55°.
On place le fil sur la graduation noire 55 de l'arc de hauteur (et non sur la graduation rouge comme dans les manipulations précédentes).
On regarde pour quelles abscisses le fil rencontre les deux lignes de la prière 'aşr. On lit ici, approximativement, les valeurs 20 et 30. Celles-ci correspondent, en degrés, à la hauteur du Soleil au moment de la prière (début et fin de la période de prière ?).
On peut retrouver le tracé de ces lignes en revenant à la règle d'Al-Bīrūnī pour l'obtention de la hauteur de 'aşr.
D'après
la règle d'Al-Bīrūnī
la hauteur h1 de la
première 'aşr est donnée par
On en déduit
.
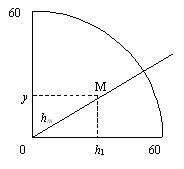
Un point M sur la ligne de première 'aşr vérifie donc :
.
La ligne de la première 'aşr a donc pour équation :
y = – x + x / tan x.
En procédant
de même, on obtient comme équation de la ligne de la 2ème 'aşr :
y = – 2x + x / tan x.
Le tracé des
courbes précédentes donne le résultat suivant (en bleu) :
Je ne suis pas sûr d'avoir épuisé les charmes mathématiques de cet instrument…