La Sphère de Jean de
Sacrobosco
CHAPITRE I
DE LA
SPHERE, DU CENTRE
d’icelle,
de l’axe ou Essieu des Pôles,
du nombre
des Sphères, & quelle est la forme du monde.
Chapitre
I.
Donc la Sphère
est ainsi décrite par Euclide. La Sphère est une marque du passage de la
circonférence d’un demi-cercle, laquelle (le diamètre demeurant fixe &
immobile) est menée & conduite tout à l’entour, jusqu’à ce qu’elle est
revenue à son premier lieu[1].
C’est à dire la Sphère est un tel rond & solide, qu’est celui qui est
décrit de l’arc du demi-cercle tourné en rond selon l’entière révolution du
cercle. La Sphère aussi par Théodose[2]
est ainsi décrite : La Sphère est une certaine chose solide contenue d’une
superficie, au milieu de laquelle est un point, duquel toutes les lignes tirées
jusqu’à la circonférence sont égales ; & ce point s’appelle le Centre
de la Sphère ; mais la ligne droite qui passe par ledit centre de la
Sphère approchant & joignant ses extrémités à la circonférence de l’une
part et de l’autre, à l’entour de laquelle la Sphère tourne, & meut,
s’appelle l’essieu de la Sphère ; mais les deux points qui terminent ledit
essieu sont nommés les pôles de la Sphère.
ANNOTATION[3].
Cette définition de la Sphère est en l’Onzième livre des
éléments d’Euclide.
La Sphère est quand ne bougeant de lieu le diamètre du
demi-cercle, et icelui demi-cercle étant contourné, revient derechef au lieu
dont cette figure a commencé à être décrite. L’intelligence de la présente définition
peut être manifestée et démontrée[4]
par les peintures ci-dessous mises. Mais quand à celle définition dont l’auteur
fait mention, elle avait été corrompue & dépravée par les interprètes de
l’Euclide écrit en Grec. Car si la ligne coulant et glissant à côté décrit
seulement une superficie, la circonférence d’un demi-cercle contournée nous
décrira la superficie du globe seulement, & non le globe massif &
solide.

Division de la Sphère du monde.
Mais la Sphère du
monde est divisée en deux manières, selon la substance, & selon l’accident.
Selon la substance en neuf Sphères. 1. C’est à savoir, en la neuvième Sphère, qui
s’appelle premier mouvement ou mobile ; en la Sphère des étoiles fixes,
qui est appelée firmament ; & es sept Sphères des sept planètes, desquelles
Sphères aucunes [= certaines] sont plus grandes, les autres moindres, selon
qu’elles sont plus prochaines, ou éloignées du firmament. Dont vient qu’entre
ces Sphères, la Sphère de Saturne est la plus grande, & la Sphère de la
Lune la moindre comme appert et est contenu en la figure suivante.
ANNOTATION.
1. En neuf Sphères, les Astrologues qui de plus
fraîche mémoire ont écrit, ils ont ajouté la dixième Sphère pour raison du
troisième mouvement qu’ils ont connu et entendu en la huitième Sphère, lequel
ils ont appelé mouvement de Trépidation[5]
ou tremblement ; & le mouvement de l’approchement &
reculement ; duquel Purbachius parle en ses Théoriques.

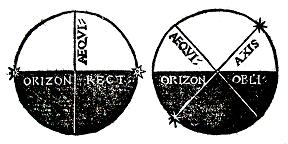
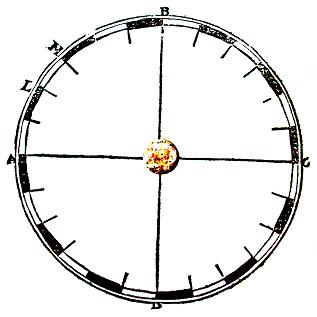
FIGURE DEMONTRANT AU
doigt le nombre, & l’ordre des Sphères célestes,
& déclarant la division du monde
selon la substance.
De la division selon l’accident.
Selon l’accident
la Sphère est divisée en droite & oblique. Ceux qui habitent sous
l’équinoxial (si quelqu’un peut demeurer en ce lieu là[6])
sont estimés avoir la sphère droite, & s’appelle droite, parce que l’un
pôle n’est pas plus élevé sur l’horizon que l’autre ; ou pour ce que leur
horizon coupe ou entrecroise l’équinoxial, & par icelui aussi ledit horizon
est entrecoupé à angles droits sphériques. Et ceux qui habitent deçà ou delà
l’équinoxial, ont la sphère oblique ; pour ce que l’un des Pôles leur est
élevé toujours sur l’horizon, & l’autre leur est ravalé & déprimé sous
le même horizon ; ou pour ce que leur horizon artificiel entrecoupe, &
divise l’équinoxial, & du même aussi il est divisé à angles inégaux et
obliques.
ANNOTATION.
Qu’est ce qu’en ce lieu ci est appelé l’horizon artificiel, tandis que les interprètes en disputent et en ont contention entre eux, tu entendras que c’est celui qui au second chapitre sera dit et nommé oblique et tranchant d’un côté.
Des parties du monde ; & quelles sont ces
parties.
L’Universelle
machine du monde est divisée en deux parties ; c’est à savoir en la région
céleste, & en la région élémentaire[7].
L’élémentaire étant continuellement ouverte & sujette à l’altération se
divise en quatre parties ; car la terre comme centre du monde, elle est
située au milieu dudit monde, à l’entour d’elle est l’eau ; à l’entour de
l’eau, l’air ; à l’entour de l’air, le feu pur et clair, lequel touche le
ciel de la Lune, comme dit Aristote au livre des Météores ; car ainsi l’a
constituée & disposée le glorieux, tout puissant & très haut Dieu.
Et ces quatre parties s’appellent
Eléments, lesquels d’eux même tour à tour s’altèrent, corrompent & se
régénèrent. Mais ces éléments sont corps simples, lesquels ne se peuvent
diviser en parties ayant diverses formes ; de la miction desquelles se
font diverses espèces des choses engendrées et produites. Or chacun des trois
environne tout à l’entour de la terre, sinon d’autant que la fixité de la terre
résiste à l’humeur de l’eau, pour la conservation & décence de la vie des
animaux ; aussi tous les éléments sont mobiles, excepté la terre, laquelle
comme étant le centre du monde, par sa pesanteur (fuyant de tous côtés
également le grand mouvement des extrémités) tient & possède le milieu de
la Sphère ronde.
De la région céleste.
A l’entour de la région
élémentaire est la région céleste, claire, & luisante ; laquelle par
son essence immuable est exempte de tout changement, & ne reçoit aucune
variété[8] ;
néanmoins tourne circulairement avec mouvement continuel ; & si est
appelée des Philosophes quinte essence, 1 à laquelle appartiennent neuf Sphères, comme ci
dessus avons dit c’est à savoir de la Lune, de Mercure, de Vénus, du Soleil, de
Mars, de Jupiter, de Saturne, des Etoiles fixes, & du dernier Ciel. Et
chacune supérieure de celle-ci environne circulairement & sphériquement
l’intérieure, & une chacune d’icelles a deux mouvements ; l’un est du
ciel dernier sur les deux bouts de l’essieu, c’est à savoir les pôles arctique
& antarctique d’Orient en Occident, retournant derechef à orient ;
& l’équinoxial divise ce mouvement par le milieu. Il y a encore un autre
mouvement des Sphères inférieures opposite à celui-ci par une obliquité sur ses
pôles distants des premiers qui sont les pôles du monde, vingt trois degrés et
trente trois minutes. 2. Mais le
premier mouvement par son impétuosité attire & ravit toutes les autres
Sphères, & en une nuit & un jour les fait mouvoir avec soi une fois à
l’entour de la terre ; combien qu’elles fassent leur effort au contraire,
comme la sphère huitième qui fait en cent ans un degré[9].
Et ce second mouvement est divisé du zodiaque par le milieu, sous lequel chacune
des sept planètes a sa propre sphère, en laquelle chacune est portée par son
propre mouvement contre le mouvement du dernier ciel, & si par le tour
qu’ils font mesurent toute la rotondité dudit ciel en divers espaces de temps,
comme Saturne en trente ans, Jupiter en douze, Mars en deux, le Soleil en trois
cent soixante cinq jours et presque six heures, Vénus & Mercure vont
semblablement quasi comme le Soleil ; mais la Lune en xxvii jours &
huit heures.

ANNOTATION.
1. Est appelée des Philosophes quinte essence, comme
Aristote en son premier livre du Ciel, qui la nomme […] c’est à dire essence
mais au livre du monde (lequel aucuns [=certains] nient être du même Aristote)
il dit […] qui signifie élément tout autre & différent de ces quatre, le feu,
l’air, l’eau, et la terre.
ANNOTATION.
2. Des premiers c’est à savoir des pôles du monde,
c’est à dire l’Arctique & Antarctique pour 23 minutes [il faut sans doute
lire 33 minutes], en ce lieu ci l’exemplaire de Faber Stapulense a seulement 51
minutes ; & ce par aventure à cause que ce nombre est écrit au second
Chapitre, où il traite des Colures & des plus petits cercles. Mais pour
autant que quasi tout ceci est pris de Ptolémée, et que les Astrologues qui
nouvellement ont écrit, ils ont observé choses diverses[10],
tu liras cela dans les Théoriques de Purbache.
Que le ciel tourne circulairement[11],
& est
de figure Sphérique.
Que le Ciel
tourne d’Orient en Occident, il appert par les étoiles qui se lèvent en Orient,
lesquelles montent peu à peu, venant successivement l’une après l’autre,
jusqu’à ce que viennent au milieu du ciel, étant toujours en même propinquité
[proximité ? ] & distance entre elles, & toujours en tel état s’en
vont continûment, & par une conformité en Occident. Il y a encore un autre
signe & argument, pris des étoiles qui sont bien près du pôle arctique
(lesquelles ne se couchent jamais en notre région, mais nous les voyons
toujours) se meuvent continuellement d’une même forme, & manière, &
décrivant leurs cercles autour du pôle, ayant toujours distance égale. Dont par
ces deux mouvements continuels tant des étoiles qui vont en Occident, que des
autres qui n’y vont point ; il est clair et manifeste que le firmament
fait son mouvement d’Orient en Occident.

De la rondeur du Ciel.
Pour trouver que
le Ciel soit rond, il y a trois raisons, similitude, commodité, & nécessité[12].
Similitude, pour ce que le monde sensible est fait à la similitude du monde
archétype I. &
originel, auquel n’y a commencement ni fin. Par quoi à la ressemblance de
celui-ci, le monde sensible ayant été fait, il a forme ronde, à laquelle ne se
peut assigner commencement ni fin. Commodité, pour ce que de tous les corps
Isopérimètres, 2. la Sphère est
la plus grande & de toutes les formes, la plus capable est la ronde ;
donc puisqu’il est rond, & encore le plus grand, s’ensuit qu’est le plus
capable.
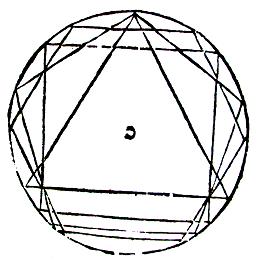
De là vient que vu que le
monde contient toutes choses, nous disons que telle forme lui a été commode
& convenable. Nécessité, car si le monde eût été d’autre forme que ronde,
c’est à savoir de forme triangulaire, carrée ou de plusieurs côtés, il
s’ensuivait deux choses impossibles :
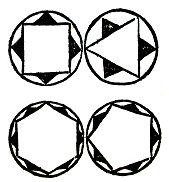
c’est à savoir, qu’il y
aurait quelque lieu vide[13],
& quelque corps sans lieu ; desquelles choses l’une et l’autre sont
fausses ; comme appert aux angles élevés et tournés alentour. Davantage
comme dit Alfragan[14],
si le ciel était de forme plate et non ronde, quelque partie d’icelui nous
serait plus prochaine que l’autre, c’est à savoir, celle qui serait sur notre
tête. 3. Donc l’étoile
qui serait là perpendiculairement sur notre tête, nous serait plus prochaine
que celle qui est en Orient ou Occident. Or les choses qui sont plus près
apparaissent plus grandes. Par quoi si le Soleil ou autre étoile était au
milieu du ciel devrait apparaître plus grand que s’il était en Orient ou en
Occident, de laquelle chose nous voyons le contraire ; car le Soleil ou
autre étoile étant en Orient ou en Occident appert plus grand que s’il était au
milieu du ciel ; mais la vérité de la chose n’est pas ainsi. La cause de
cette apparence[15] est, qu’au
temps d’hiver ou pluvieux, certaines vapeurs montent entre notre regard &
le Soleil ou autre étoile. Et comme ainsi soit, que ces vapeurs soient un corps
4. diaphane ou transparent,
elles désagrègent & séparent nos rayons visuels, en sorte que ne
comprennent la chose en sa naturelle & vraie quantité, comme appert d’un
denier jeté au fond d’une eau claire, lequel à cause de la désagrégation des
rayons apparaît de plus grande quantité qu'il n'est.
ANNOTATION.
1. Archétypos substantif est la première forme,
l’idée, le patron que nous devons imiter. En ce lieu il signifie cette forme du
monde de laquelle Dieu par sa prescience a conçu en son entendement qu’il ferait
ce monde, et cette cogitation de Dieu, est éternelle, comme Dieu même est
éternel. Et d’autant que Dieu est sans commencement & fin, il est à
présupposer que créant les cieux, il leur a donné forme ronde qui est figure en
laquelle on ne peut connaître le commencement ni la fin[16].
ANNOTATION.
2. Iso égale, peri à l’entour, métron mesure,
perimetros la ligne environnant est le circuit ou le tour de quelque chose. Si
donc il était deux îles, par manière de dire, ayant chacune vingt stades de
circuit ; l’une desquelles soit triangulaire et l’autre ronde tellement
qu’elle aie la forme d’un cercle, de toutes ces deux isopérimètres, c’est à
dire qui se peuvent mesurer [égales] à l’entour, la plus grande & celle qui
le plus contiendra ce sera la ronde. Tout ainsi en adviendra si d’une même
terre gluante comme terre de potier tu fais un vaisseau rond puis de rond
carré. Théon nous démontre ceci en Ptolémée au premier livre de sa grande
construction[17].
ANNOTATION.
3. Ton Alfragan en la seconde différence se joue, car
les cieux contournés en rond, un chacun point toujours également distant de
centre, changerait de lieu & mouvrait son ordre. Ceci a annoté Pierre
Nonius.
ANNOTATION.
4. Diaphane, je ne sais si Rodiginus l’a lu en
quelques auteurs approuvé ; quant est de moi j’ai mémoire d’avoir
seulement lu diaphanes. Car diaphanes en Grec sont l’air, l’eau, le verre, le
cristal, les vapeurs et autres telles choses semblables, tellement rare &
détenue substance qu’on peut voir tout au travers sans empêchement. J’estime
que les Latins ont dit Pellucidum, comme le crible et la lanterne punique et un
agneau tellement maigre, que vivant et se tenant au Soleil, on lui pouvait voir
toutes les entrailles de son corps. Plaute en sa Ruden & Aulul. a dit
Pellucere. Mais pourquoi les effigies & figures sont vues dans l’eau plus
grandes, qu’elles ne sont véritablement, Macrobe le dispute en son septième
livre des Saturnales.
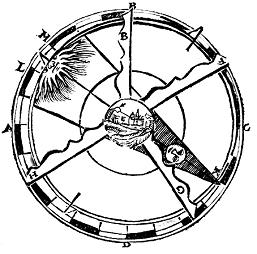
La déclaration du précédent argument, se
montre par les figures suivantes.
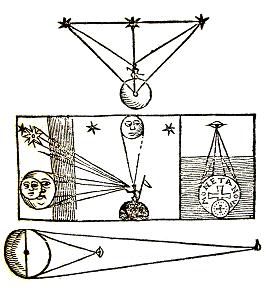
La rondeur de la terre
nous est manifeste ainsi que s’ensuit[18].
Les signes du zodiaque, & autres étoiles ne se lèvent et couchent d’une
même façon et manière à tous les hommes qui habitent la terre en divers
lieux ; ainsi se lèvent & couchent premièrement à ceux qui sont plus
prochain d’Orient. Et que à quelques uns elles se lèvent & couchent plus
tôt, ou plus tard, l’enflure & tumeur de la terre en est cause ; comme
il appert très bien par les choses qui se font au ciel ; car une même
éclipse de Lune qui s’apparaît à nous en la première heure de la nuit apparaît
aux Orientaux environ la troisième heure d’icelle même nuit.
Il est donc évident qu’ils
ont eu plus tôt la nuit, & que le Soleil couche plus tôt à eux qu’à nous.
Tout cela vient seulement de la tumeur de la terre. Considère la précédente
figure pour mieux entendre ce qui a été dit ci-dessus[19].
Que la terre aussi soit
ronde de Septentrion vers Midi, & de midi venant à Septentrion, on le
connaît ainsi. Aux hommes qui sont vers Septentrion certaines étoiles apparaissent
toujours, c’est à savoir celles qui sont plus prochaines du pôle arctique,
& les autres au contraire leur sont toujours cachées, c’est à savoir celles
qui sont près du pôle antarctique. Si donc quelqu’un cheminait de septentrion
vers midi, il pourrait tant aller que les étoiles premières qui lui étaient
apparentes toujours, lui seraient cachées[20] ;
& tant plus qu’ils s’approcherait du Midi, d’autant plus lesdites étoiles
lui seraient rabaissées sous l’horizon ; & icelui même homme
commencerait à voir les étoiles qui auparavant lui étaient cachées. Le
contraire pourrait advenir à quelqu’un qui irait du Midi à Septentrion. La
cause de ceci est seulement la tumeur de la terre. Davantage si la terre était
plane d’Orient en Occident, aussi tôt se lèveraient les étoiles aux Occidentaux
comme aux Orientaux, ce qu’appert être faux. En outre si la terre était plane
de Septentrion à midi , & de Midi à Septentrion, les étoiles apparentes à
celui qui serait en Septentrion, lui seraient toujours apparentes vers quelque
lieu qu’il cheminât, ou en quelque lieu qu’il fût ; ce qu’on voit être
faux. Encore qu’il semble à la vue des hommes que la terre est plane ;
mais cela advient pour raison de sa grande quantité.
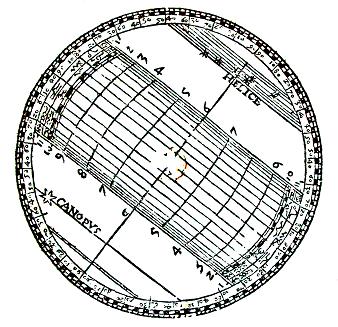
Instrument par lequel est
prouvée la rondeur de la terre selon la latitude, & est déclaré facilement
tout ce que l’auteur traite au troisième Chapitre des jours artificiels.

Que l’eau soit ronde.
Que l’eau ait
tumeur s’approchant d’une rotondité il appert ainsi ; qu’on mette une
marque au bord de la mer, & que le navire partant du port s’éloigne ;
tant que l’œil d’icelui qui est au pied du mât ne puisse voir ladite marque,
& le navire étant arrêté, l’œil d’icelui qui sera au sommet du mât verra
très bien icelle marque ; toutefois l’œil de celui qui est près du pied du
mât devrait voir mieux la marque, que celui qui est au sommet du mât, comme
appert par les lignes tirées desdits lieux à la marque. La cause de ceci n’est
autre, sinon que la rondeur et tumeur de l’eau. Soient ôtés tous autres
empêchements, comme brouillards, nuées, & les vapeurs qui montent.
Davantage comme ainsi soit que l’eau est un corps 1. Homogène, duquel les parties ont une même raison
& appellation avec le tout, s’ensuit que tout le corps sera de la même
espèce avec ses parties ; or les parties de l’eau (comme il advient es
gouttelettes de la rosée du ciel, qui sont sur les feuilles des arbres &
herbes) appètent naturellement la forme ronde ; par quoi tout le corps
aussi, duquel elles sont les parties.
ANNOTATION.
1. Homogène, de même genre & nature, pris du Grec.
Mais la terre et l’eau font et constituent un globe[21],
et quelquefois on a douté laquelle de ces parties était la plus grande. Aucuns
ont pensé que c’était l’eau ; mais ceux qui naguère sont allés à l’entour
de la terre, pour la voir de tous côtés, & l’ont décrite, s’ils ne nous
déçoivent & abusent ; ils disent que la face de la terre est plus
grande que celle de l’eau ; de quoi notre Nonius même nous admoneste et
avertit[22].

Que la terre est le centre du monde, &
qu’elle demeure immobile.
Que la Terre soit
située au milieu du firmament il appert ainsi. A ceux qui sont en la superficie
de la terre, les étoiles apparaissent d’une même quantité, soient elles au
milieu du ciel près d’Orient ou près d’Occident ;

& cela advient à cause
que la terre est également distante d’icelles ; car si la terre était plus
prochaine du firmament en une part qu’en autre, s’ensuivrait que celui qui
serait en une partie de la superficie de la terre plus prochaine du firmament
ne verrait la moitié du ciel ; ce qui est contre l’opinion de Ptolémée[23]
& de tous les philosophes, qui disent, que en quelque lieu de la terre où
l’homme puisse être, six signes du zodiaque lui sont élevés, & les autres
six couchés, & par ainsi toujours la moitié du ciel lui est apparente,
& l’autre moitié lui demeure cachée.
Semblablement nous avons
marque & signe évident que la terre est comme un centre et point, ayant
égard au firmament ; car si la terre était de quelque quantité auprès du
firmament, la moitié du ciel ne se pourrait voir. Davantage si l’on entend une
superficie plane sur le centre de la terre, divisant icelle en deux parties
égales, & par conséquent le firmament, lors l’œil qui serait au centre de
la terre verrait la moitié du ciel, & icelui même œil étant en la
superficie de la terre verrait la même moitié du ciel.

Des choses susdites s’ensuit
que la quantité de la terre, qui est depuis la superficie jusqu’au centre, est
insensible, & par conséquent la quantité de la terre au regard du firmament[24].
Aussi Alphragant [autre orthographe] dit que la moindre des étoiles fixes, qui
se puisse voir, est plus grande que toute la terre ; mais icelle étoile,
ayant égard au firmament, est comme un point & centre ; par plus forte
raison la terre sera un point, au regard d’icelui, vu qu’elle est moindre
qu’icelle étoile.
Que la terre soit immobile,
& située au milieu du monde, vu qu’elle est fort pesante, il nous est donné
à entendre par sa pesanteur ; car toute chose pesante tend naturellement
au centre[25] ; le centre
est un point au milieu du firmament. La terre donc vu qu’elle est de grande
pesanteur, tend naturellement à icelui point.
Item toute chose qui est
tirée ou se meut hors le centre & point du milieu, monte à la circonférence
du ciel. Si donc la terre se meut du centre & milieu du ciel, elle monte à
la circonférence d’icelui ; ce qu’on laisse pour impossible.
Du circuit de la terre, & de
son diamètre.
Tout le circuit
de la terre, selon Ambroise, Théodose, Macrobe[26],
& Eratosthène philosophes, contient 252 000 stades, comptant pour chacune
de 360 parties du Zodiaque sept cents stades ; ce qu’on pourra
expérimenter prenant l’astrolabe ou quadrant en une nuit bien claire &
étoilée ; voyant le pôle par les deux trous des pinnules, faudra noter le
nombre des degrés, qui nous sera montré par le mediclin dit en Arabe Alhidade
[alidade].
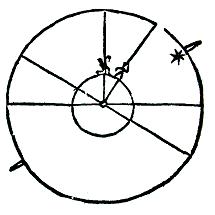
En après celui qui mesure le
monde faut qu’il
procède et chemine par ligne droite de Midi à Septentrion, jusqu’à ce qu’en la
clarté d’une autre nuit, voyant le pôle comme auparavant il ait mis le mediclin
[l’alidade] plus haut d’un degré. Puis après avoir mesuré l’espace du chemin
qui est entre la première & seconde observation & seront trouvés 700
stades ; ceci bien connu et entendu si baillez à chacun des trois cent
soixante degrés, autant de stades, le circuit de la terre sera entièrement
trouvé[27].

Otez la
vingt deuxième partie du circuit de la terre, & la troisième partie de ce
que reste, c’est à savoir octante mille cent octante un stades & demi,
& la troisième partie d’un stade, sera le diamètre ou épaisseur de la terre[28].
ANNOTATION.
Ambroise, Théodose, Macrobe, en ce lieu ici est un même auteur. C’est à savoir ce Macrobe, qui a écrit les livres des Saturnales, & les commentaires sur le Songe de Scipion ; dans lesquels au livre premier vous trouverez ce qui a été dit du circuit de la terre comme pris de Eratosthène. Je ne sais pourtant si de Sacrobosco a vu & lu les écrits de icelui Eratosthène, lesquels si nous les eussions pu recouvrer & fussent tombés entre nos mains tous entiers, nous saurions qu’il a écrit, & veut le circuit de la terre être de deux cent cinquante et deux milles stades, comme nous récite & raconte Pline sur la fin de son second livre & le susdit Macrobe, Capella et aussi de Sacrobosco ; mais si c’est de deux cent cinquante [milles] seulement, c’est à dire en Grec […], ainsi que contient le premier livre de Cléomèdes. Et certes l’autorité ouïe de celui-ci seul doit avoir grand poids et peut servir de beaucoup à cause qu’il amène les raisons & fait les mêmes démonstrations de Eratosthène.
Ptolémée après Eratosthène a été celui qui pour sept cents stades a ordonné cinq cents stades seulement à un chacun degré du terrestre méridien répondant à un degré méridien céleste ; la grandeur de la terre étant inconnue pour raison de la grande difficulté qui est de bien mesurer, ou bien si tu veux estimer & chercher ladite mesure en terre comme Eratosthène et d’autres ; ou en la mer comme Posidoine [Posidonios] et le même Cléomède auteur[29]. Ce que en ce lieu ci est simplement & vulgairement appelé le circuit de la terre, il n’est pas de la seule terre mais de la terre et de l’eau ensemble, parce que l’eau et la terre joints en un & non séparés, sont estimés faire & constituer une Sphère ronde [au lieu de deux]. Au reste les Géomètres ont fait les vers suivants qui parlent des mesures, afin que plus facilement on les peut mettre en mémoire, pour s’en resouvenir quand on en a besoin.
De quatre grains est la largeur d’un doigt,
En quatre doigts toute palme est parfaite,
Et quatre paumes un pied contenir doit,
Cinq pieds aussi à un pas faut qu’on mette,
Cent vingt cinq pas est la mesure faite
Pour un seul stade, & toujours on entend
Qu’un millier a huit stades complets,
Deux milliers la lieue aussi comprend.
Si est-ce que la lieue qui
est un mot Français, duquel aussi les Espagnols usent, ne contient point deux
milliers, mais un & demi seulement, c’est à savoir mille cinq cents pas,
comme nous en baille la définition Ammianus Marcellinus en son quinzième et
seizième livres, & Iornandus en son traité des choses Gothiques. En outre
les Géomètres ont encore bien peu démontré certaine raison ou proportion de la
quantité du circuit de quelque cercle que ce soit avec son diamètre. Combien
que en attendant mieux, pour la vraie proportion vulgairement a été reçue celle
qu’on a nommé triple sesquiseptième, tout ainsi que 22 sont à 7[30].
En cette façon et manière les vers suivants enseignent comment par la
connaissance du diamètre nous devons trouver la circonférence, ou circuit du
cercle, et au contraire sachant la quantité dudit circuit, soudain et sans
grand peine nous démontre la quantité du diamètre.
D’un rond qui veut
savoir le diamètre
Par sept le tout
multiplier il doit,
Puis en portions par
vingt et deux faut mettre,
Tout le produit &
quotient qu’il voit,
Pour diamètre il peut
prendre à bon droit.
Mais s’il voulait le
diamètre étendre,
Grand besoin est que
multiplié soit
Par vingt & deux,
puis le sept il faut prendre
Pour diviser, afin qu’il
puisse rendre
D’un cercle entier le
tout qu’on demandait.
> Retour vers la page
Sacrobosco