POURQUOI LE CADRAN DE REGIOMONTANUS FONCTIONNE-T-IL ?

Vers la fin de sa carrière, le grand astronome Jean Baptiste Joseph Delambre (1749-1822), connu pour la mesure du méridien lors de la détermination du mètre, s'intéressa à l'histoire de l'astronomie et publia six imposants volumes sur le sujet. Le volume de l'Histoire de l'astronomie au Moyen-Age est paru en 1819. Delambre, impressionné par l'ingéniosité du cadran universel de Regiomontanus, cherche à en comprendre l'origine.

Nous reprenons ici sa démarche, en modernisant la présentation et en essayant d'être aussi clair que possible… Les citations, en italiques, sont extraites de l'ouvrage de Delambre.

Regiomontanus ne fournit pas la clé

Dans les éditions posthumes du Calendrier de Regiomontanus (Kalendarium magistri Joannis de Monte-Regio…), on trouve une description du cadran universel (nommé Quadratum horarium generale), ainsi qu'une planche munie d'un bras mobile en laiton.

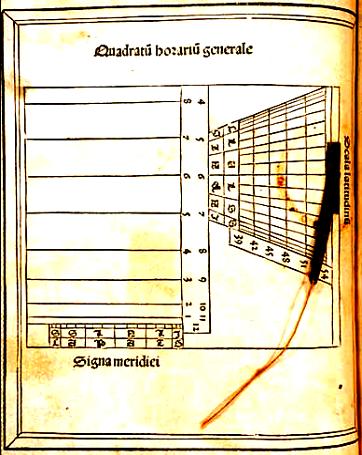
L'édition consultée par Delambre est de 1499 : "En quelque habitation que vous soyez, vous trouverez les heures du jour par le carré horaire inséré dans ce livre."

Cependant, si Regiomontanus donne une description précise des tracés, il ne les explique en rien. Delambre note qu'il "faut absolument deviner. Il n'est donc pas bien étonnant que la démonstration ait été longtemps omise et sans doute ignorée de tous les auteurs de Gnomonique."

"Regiomontanus ne s'attribue pas cette invention ; il n'en nomme point l'auteur, mais l'étude particulière qu'il avait faite des livres arabes nous persuade qu'il tenait cette invention d'un auteur de cette nation."

"En lisant l'ouvrage d'Aboul Hassan sur la Gnomonique, traduit par M. Sedillot, il m'avait paru que les Arabes avaient des instruments qui leur donnaient l'heure sans calcul par une seule ombre du Soleil. J'avais cherché quelle pouvait être la construction de l'instrument des Arabes, et comment on pourrait remonter au principe de l'analemme universel [le cadran de Regiomontanus], exposé par tous les auteurs [Munster, Finé, Clavius…] sans aucune démonstration."

"Les Arabes avaient l'équivalant de notre formule

,

ils avaient des tangentes et des sécantes, qu'ils avaient introduites non seulement dans la Gnomonique, mais même dans la trigonométrie ; ils avaient plus de moyens que Regiomontanus pour imaginer l'analemme universel ; et si Regiomontanus est le premier qui l'ait fait connaître aux Européens, il a pu le tenir des Arabes, dont il avait étudié les ouvrages. Il est possible qu'un de ces analemmes lui soit tombé entre les mains, et qu'il l'ait reçu d'Espagne, où les Arabes l'avaient apporté ; il en aura donné la figure et les usages, sans peut-être se donner la peine d'en chercher la démonstration."

Ceci, du moins, est l'hypothèse de Delambre.

Le principe de l'analemme universel, selon Delambre

"Le problème général à résoudre pour trouver la construction de cet analemme, se compose de trois parties distinctes.

· 1°– De tracer et espacer convenablement les lignes horaires.

· 2°– De trouver le point de suspension, ou le lieu de la main qui porte le fil, pour parler comme Regiomontan. Ce point de suspension doit varier avec la hauteur du pôle du monde [la latitude] et avec la déclinaison du Soleil.

· 3°– De déterminer pour chaque déclinaison et pour chaque hauteur du pôle, à quelle distance du point de suspension, la perle ou le nœud mobile doit être arrêté pour marquer l'heure pendant la journée."

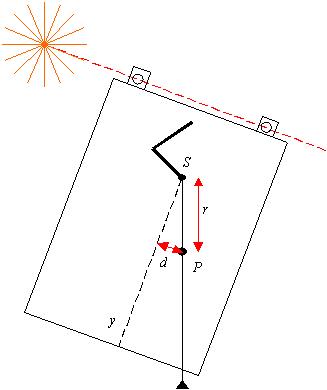
On désigne par S le point de suspension, par P la position de la perle, lorsqu'elle marque l'heure, et on note (Sy) l'axe mené par S et perpendiculaire à celui des pinnules.

On note r la distance SP et d la distance entre la perle et l'axe (Sy).

L'angle de hauteur h du Soleil au dessus de l'horizon, se retrouve entre l'axe (Sy) et le fil (SP).

On a donc : d = r sin h (1).

On note j la latitude, d la déclinaison du Soleil et H l'angle horaire (compté sur l'équateur à partir de midi).

L'analemme consiste à reconstituer la formule de trigonométrie sphérique :

(*).

D'après (1), on doit faire en sorte que :

.

Ou encore :

.

L'idée, selon Delambre, est de placer S et P pour avoir :

,

et :

.

De cela résulte une "construction, qui est sans doute celle de Regiomontanus." C'est du moins ce que suppose Delambre.

1^er point : les lignes horaires

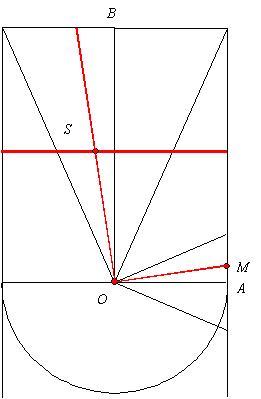
"D'un rayon arbitraire que vous prendrez comme unité, décrivez un cercle occulte qui représentera l'équateur."

Il s'agit, sur la figure, du demi-cercle de centre O et de rayon [OA]. Il est "occulte" en ce sens que son tracé sur le cadran n'est pas indispensable. D'ailleurs il n'apparaît pas sur la figure de Regiomontanus. Il "représente l'équateur" en ce sens que l'on prend dessus un angle tous les 15° pour tracer les lignes horaires verticales. L'angle horaire H est mesuré en O, à partir de [OA]. La verticale menée par A correspond à midi. La verticale menée en dessous de O correspond à la ligne horaire de 6h (H = –90°) et 18h (H = +90°).

On gradue le diamètre horizontal tous les 15° , c'est à dire tous les cos H à partir de O, avec H = 0°, 15°, 30°, etc.

Par tous ces points on trace des parallèles aux lignes de 12h et 6h "et le premier point sera résolu."

2^ème point : le point de suspension

On forme en haut de la figure le "trigone des signes" en prenant un angle BÔS égal à la déclinaison d.

On trace une horizontale à la distance tan j de O. C'est la ligne de latitude, ou, selon Regiomontanus, le "zodiaque d'habitation". C'est le lieu "des points de suspension pour l'année".

Le point de suspension S est situé à l'intersection avec la droite correspondant à la déclinaison d du jour.

On vérifie que la distance entre S et l'axe (OB) est donnée par tan j ´ tan d . Ainsi, lorsque la perle est sur la ligne horaire d'angle horaire H, elle est bien à une distance d de l'axe (OB) vérifiant :

.

De plus, on a :

.

Cela résout le second point.

3^ème point : distance r point de suspension – perle

Il reste à mesurer la distance r entre la perle et le point S de sorte que :

.

Or on a :

.

D'où :

.

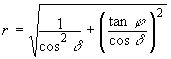On obtiendra r comme l'hypoténuse d'un triangle rectangle dont un côté mesure
tanj / cosd (c'est justement le cas de OS) et l'autre côté mesure 1 / cos d.

On obtient une perpendiculaire à [OS] en prenant en O un angle d à partir de l'horizontale [OA]. Puisque OB = 1, le point M obtenu à l'intersection avec la ligne de midi vérifie :

.

On a donc r = SM.

Ceci explique la construction du "second trigone des signes" à la droite de la ligne de midi.

"Ainsi, quand le fil sera arrêté par un bout au point de suspension, […] conduisez ce fil au zodiaque de midi, au point de déclinaison ; arrêtez la perle à ce point ; l'instrument sera préparé pour l'observation."

[…]

"Notre équation générale (*) est susceptible de plusieurs constructions. […] une seconde [est celle] du jésuite St-Rigaud, qui l'a publiée sous le titre d'Analemma novum."

Retour au cadran de Regiomontanus