Sur le quadrant des sinus
(al-Khwarizmi)

Le texte suivant (issu du même manuscrit de Berlin que les précédents) contient la première description connue du « quadrant des sinus ».

Les traducteurs, F. Charette et Petra G. Schmidl, pensent pouvoir l’attribuer raisonnablement à al-Khwarizmi, en raison du style du texte et du fait que la base choisie pour l’échelle des sinus (de 0 à 150), une base trigonométrique indienne, est celle utilisée dans les textes d’al-Khwarizmi.

Un dernier argument en faveur d’al-Khwarizmi est fourni par l’astronome du XIII^e siècle al-Marrakushi qui dans son traité (Traité des instruments astronomiques des arabes – traduction Sédillot XIX^e siècle) nous apprend que certaines personnes nomment le quadrant des sinus, al-jayb al-khwarizmi, c’est-à-dire le (quadrant) des sinus d’al-Khwarizmi.

TEXTE : Al-Khwarizmi « Sur le quadrant des sinus », manuscrit de Berlin folio 96 verso – 97 verso

(d’après la traduction en anglais de F. Charette et Petra G. Schmidl - 2004.)

La construction d’un quadrant avec lequel on peut déterminer le sinus, la déclinaison, et les heures du jour qui se sont écoulées.

Si vous voulez faire ce quadrant – avec l’aide et la bénédiction de Dieu – un quadrant de [... texte manquant...] fait à angles droits, sortant du cercle de la plaque graduée. Puis divisez le en 90 parties (égales). Divisez (la ligne allant) du centre (du quadrant) à l’extrémité des 90 parties, en 150 parties, chaque partie égale. C’est l’(échelle du) sinus. Ensuite suspendez-y (au centre) un fil avec un plomb. Puis faites sur (l’échelle du) sinus (une marque de graduation) pour le sinus de chaque degré en suivant ce qui est dans la table préparée (à cette intention). (Ceci) peut-être déterminé convenablement à partir de la table consignée dans la table des sinus. Afin de savoir cela vous devez prendre le sinus de (chacun) des 5 degrés de hauteur. Regardez à combien d’unités du sinus c’est. Tracez une ligne (correspondant à ceci) à l’intérieur du quadrant sur la plaque comme vous le voyez représenté. Sachez ceci – Selon la très Grande Volonté de Dieu !

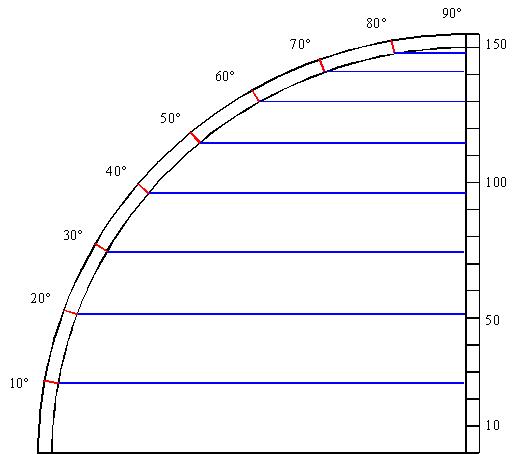
(représentation tous les 10° - al-Khwarizmi représente le sinus tous les 5°)

La suite du texte présente une utilisation du quadrant des sinus pour passer de la longitude du Soleil sur l’écliptique (angle mesuré sur l’écliptique à partir du point g) à sa déclinaison (en Nord/Sud par rapport à l’équateur). Cette utilisation suppose l’existence sur le quadrant d’un quart de cercle « rouge », arc de l’obliquité de l’écliptique, dont le rayon correspond au sinus de l’obliquité de l’écliptique.

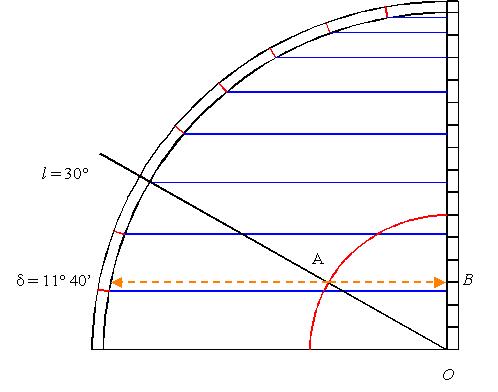
La description de l’utilisation de ce quadrant une fois construit.

Si vous voulez déterminer la déclinaison de chaque degré (de longitude), faites exactement comme je vous le décris. Si nous voulons déterminer la déclinaison de la fin du Bélier, nous plaçons le fil sur le côté de la 30^e division de hauteur. Puis regardez à quel endroit sur le cercle rouge – le cercle de déclinaison – le fil tombera. Puis prenez là la direction (du sinus le long des lignes horizontales). Nous trouvons que le fil que nous avons pris là tombe sur 25 degrés [sic ! – la valeur attendue de la déclinaison de 30° de longitude est 11°40’] et quelques minutes des 90 degrés. C’est la déclinaison du Bélier. De même, si vous voulez la déclinaison de (la fin du) Taureau, prenez ce qui est en face de 60 (unités) de l’altitude (sur le cercle de déclinaison), opérez avec ceci de la même manière. La déclinaison de (la fin des) Gémeaux – (dont la longitude) est de 90 degrés – est la complète déclinaison (par exemple l’obliquité). La déclinaison de la fin du Cancer est la même que la déclinaison du début des Gémeaux. L’opération ave les (signes zodiacaux) restants est semblable.

[...]

Si vous voulez opérer avec un sinus sexagésimal, divisez l’(échelle) de sinus du quadrant en 60 (divisions).

Explication

La présence de cercle « rouge » laisse à penser que le quadrant décrit est de bois plutôt que de métal, comme le sont les quadrants ottomans que l’on rencontre jusqu’au XX^e siècle (à ce propos, voir quadrant ottoman.htm ).

La formule reliant la déclinaison d du Soleil à sa longitude l est la suivante :

sin d = sin e ´ sin l .

En prenant comme obliquité de l’écliptique e = 23°30’ et une base de sinus de 150, on obtient comme rayon pour le cercle « rouge » : r = sin e ´ 150 » 59,8 (voir la figure ci-dessus).

Dans le premier exemple, le Soleil est à la fin du premier signe zodiacal, c’est-à-dire que sa longitude est l = 30°.

On place donc le fil du quadrant sur la graduation 30°.

Le fil coupe le cercle rouge au point A.

Si B est la projection orthogonale de A sur le bord vertical du cadran, on a :

OB = OA ´ sin l = sin e ´ sin l .

OB = sin d .

On en déduit que la déclinaison d du Soleil est à lire horizontalement sur le bord circulaire du quadrant.

Soit, dans cet exemple, une déclinaison d d’un peu plus de 11° (Nord puisqu’on est au début du printemps).

Retour à la page "Al-Khwarizmi et l'astrolabe"