AVENTURES DE TROIS RUSSES
ET DE TROIS ANGLAIS
EN AFRIQUE AUSTRALE

Douzième voyage extraordinaire : 1871/1872.

Chapitre III

[…]

A six heures du matin, le colonel Everest donna le signal du départ. Passagers et marins s'embarquèrent sur le Queen and Tzar. Le chasseur, à qui la route du fleuve était familière, les suivit à bord, laissant aux deux bochesjmens le soin de ramener le chariot à Lattakou.

Au moment où l'embarcation larguait son amarre, le colonel Everest dit à l'astronome :

"A propos, monsieur Emery, vous savez ce que nous venons faire ici ?

– Je ne m'en doute même pas, colonel.

– C'est bien simple, monsieur Emery. Nous venons mesurer un arc de méridien dans l'Afrique australe."

Chapitre IV – Quelques mots à propos du mètre

De tout temps, on peut l'affirmer, l'idée d'une mesure universelle et invariable, dont la nature fournirait elle-même la rigoureuse évaluation, a existé dans l'esprit des hommes. Il importait, en effet, que cette mesure pût être exactement retrouvée, quelque fussent les cataclysmes dont la terre aurait été le théâtre. Très certainement, les anciens pensèrent ainsi, mais les méthodes et les instruments leur manquèrent pour exécuter cette opération avec une approximation suffisante.

Le meilleur moyen, en effet, d'obtenir une immuable mesure, c'était de la rapporter au sphéroïde terrestre, dont la circonférence peut être considérée comme invariable, et par conséquent, de mesurer mathématiquement tout ou partie de cette circonférence.

Les anciens avaient cherché à déterminer cette mesure. Aristote, d'après certains savants de son époque, considérait le stade, ou coudée égyptienne au temps de Sésostris, comme formant la cent millième partie du pôle à l'équateur. Eratosthène, au siècle des Ptolémées, calcula d'une manière assez approximative la valeur du degré le long du Nil, entre Syène et alexandrie. Mais Posidonius et Ptolémée ne purent donner une exactitude suffisante aux opérations géodésiques du même genre qu'ils entreprirent. De même, leurs successeurs.

Ce fut Picard qui, la première fois en France, commença à régulariser les méthodes employées pour la mesure d'un degré, et en 1669, déterminant la longueur de l'arc céleste et de l'arc terrestre entre Paris et Amiens, il donna pour la valeur d'un degré cinquante sept mille soixante toises.

La mesure de Picard fut continuée jusqu'à Dunkerque et jusqu'à Collioure par Dominique Cassini et Lahire, de 1683 à 1718. Elle fut vérifiée, en 1739, de Dunkerque à Perpignan, par François Cassini et Lacaille. Enfin, la mesure de l'arc de ce méridien fut prolongée par Méchain jusqu'à Barcelone en Espagne. Méchain étant mort, - il succomba aux fatigues provoquées par une telle opération, - la mesure de la méridienne de France ne fut reprise qu'en 1807 par Arago et Biot. Ces deux savants la poursuivirent jusqu'aux îles Baléares. L'arc s'étendait alors de Dunkerque à Formentera ; son milieu se trouvait coupé par le quarante-cinquième parallèle nord, situé à la même distance du pôle et de l'équateur, et dans ces conditions, pour calculer la valeur du quart de méridien, il n'était pas nécessaire de tenir compte de l'aplatissement de la terre. Cette mesure donna cinquante-sept mille vingt-cinq toises pour la valeur moyenne d'un arc d'"un degré" en France.

On voit que jusqu'alors, c'était spécialement des savants français qui s'occupaient de cette détermination délicate. Ce fut aussi la Constituante qui, en 1790, sur proposition de Talleyrand, rendit un décret par lequel l'Académie des Sciences était chargée d'imaginer un modèle invariable pour toutes les mesures et pour tous les poids. A cette époque, le rapport signé de noms illustres, Borda, Lagrange, Laplace, Monge, Condorcet, proposa pour mesure de longueur usuelle la dix millionième partie du quart de méridien, et pour évaluation de la pesanteur de tous les corps, celle de l'eau distillée, le système décimal étant adopté pour relier toutes les mesures entre elles.

Plus tard, ces déterminations de la valeur d'un degré terrestre furent faites en divers lieux de la terre, car le globe n'étant pas un sphéroïde, mais un ellipsoïde, des opérations multiples devaient donner la mesure de son aplatissement aux pôles.

En 1736, Maupertuis, Clairaut, Camus, Lemonnier, Outhier et le suédois Celsius mesurèrent un arc septentrional en Laponie et trouvèrent cinquante-sept mille quatre cent dix-neuf toises pour la longueur d'un arc d'un degré.

En 1745, au Pérou, La Condamine, Bouguer, Godin, aidés des Espagnols Juan et Antonio Ulloa, accusèrent cinquante-six mille sept cent trente-sept toises pour la valeur de l'arc péruvien.

En 1752, Lacaille rapporta cinquante-sept mille trente-sept toises pour la valeur d'un degré du méridien au cap de Bonne-Espérance.

En 1754, les pères Maire et Boscowith obtinrent cinquante-six mille neuf cent soixante-treize toises pour la valeur de l'arc entre Rome et Rimini.

En 1762 et 1763, Beccaria évalua le degré piémontais à cinquante-sept mille quatre cent soixante-huit toises.

En 1768, les astronomes Masson et Dixon, dans l'Amérique du Nord, sur les confins du Maryland et de la Pennsylvanie, trouvèrent cinquante-six mille huit cent quatre-vingt-huit toises pour la valeur du degré américain.

Depuis, au XIX^e siècle, nombre d'autres arcs furent mesurés, au Bengale, dans les Indes Orientales, au Piémont, en Finlande, en Courlande, dans le Hanovre, dans la Prusse orientale, en Danemark, etc. ; mais les Anglais et les Russes s'occupèrent moins activement que les autres peuples de ces déterminations délicates, et la principale opération géodésique qu'ils firent fut entreprise, en 1784, par le major général Roy, dans le but de relier les mesures françaises aux mesures anglaises.

De toutes les mesures ci-dessus relatées, on pouvait déjà conclure que le degré moyen devait être évalué à cinquante-sept mille toises, soit vingt-cinq lieues anciennes de France, et en multipliant par cette valeur moyenne les trois cent soixante degrés que contient la circonférence, on trouvait que la terre mesurait neuf mille lieues de tour.

Mais, on l'a pu voir par les chiffres rapportés ci-dessus, les mesures des divers arcs obtenus en divers lieux du globe ne concordaient pas absolument entre elles. Néanmoins, de cette moyenne de cinquante-sept mille toises prise pour la mesure d'un degré, on déduisit la valeur du "mètre", c'est à dire la dix millionième partie du quart du méridien terrestre, qui se trouve être de 0,513074, soit trois pieds onze lignes deux cent quatre-vingt-seize millièmes de ligne.

[…]

Le mètre, ainsi déterminé, ne fut cependant pas adopté par toutes les nations civilisées. La Belgique, l'Espagne, le Piémont, la Grèce, la Hollande, les anciennes colonies espagnoles, les républiques de l'Equateur, de la Nouvelle-Grenade, de Costa Rica, etc., l'admirent presque immédiatement ; mais malgré la supériorité presque évidente du système métrique sur tous les autres systèmes, l'Angleterre s'est refusée jusqu'à ce jour à l'adopter.

Peut-être, sans les complications politiques qui marquèrent la fin du XVIII^e siècle, ce système eût-il été accepté par les populations du Royaume-Uni. Quand, le 8 mai 1790, l'Assemblée constituante rendit son décret, les savants anglais de la Société royale furent invités à se joindre aux savants français. Pour la mesure du mètre, on devait décider si elle serait fondée sur la longueur du pendule simple qui bat la seconde sexagésimale, ou si l'on prendrait comme unité de longueur une fraction de l'un des grands cercles de la terre. Mais les évènements empêchèrent la réunion projetée.

Ce ne fut qu'en cette année 1854, que l'Angleterre, comprenant depuis longtemps les avantages du système métrique, et voyant d'ailleurs des sociétés de savants et de commerçants se fonder pour propager cette réforme, résolut de l'adopter.

Mais le gouvernement anglais voulut tenir cette résolution secrète jusqu'au moment où de nouvelles opérations géodésiques, entreprises par lui, permettrait d'assigner au degré une valeur plus rigoureuse. Cependant, à cet égard, le gouvernement britannique cru devoir s'entendre avec le gouvernement russe qui penchait aussi pour l'adoption du système métrique.

Une commission, composée de trois astronomes anglais et de trois astronomes russes, fut donc choisie parmi les membres les plus distingués des sociétés scientifiques. On l'a vu, ce furent pour l'Angleterre, le colonel Everest , sir John Murray et William Emery ; pour la Russie, MM. Mathieu Strux, Nicolas Palander et Michel Zorn.

Cette commission internationale réunie à Londres, décida que tout d'abord la mesure d'un arc du méridien serait entreprise dans l'hémisphère austral. Cela fait, un nouvel arc du méridien serait ensuite relevé dans l'hémisphère boréal, et de l'ensemble de ces deux opérations, on espérait déduire une valeur rigoureuse qui satisferait à toutes les conditions du programme.

[…]

Il convient aussi d'ajouter qu'à côté de la question scientifique, il y avait une question d'amour-propre national qui exaltait ces savants réunis dans une œuvre commune. Il s'agissait, en effet, de surpasser la France dans ses évaluations numériques, de vaincre en précision les travaux de ses plus illustres astronomes, et cela au milieu d'un pays sauvage et presque inconnu. Aussi les membres de la commission anglo-russe étaient-ils décider à tout sacrifier, même leur vie, pour obtenir un résultat favorable à la science et en même temps glorieux pour leur pays.

Et voilà pourquoi, dans les derniers jours de janvier 1854, l'astronome William Emery se trouvait aux chutes de Morgheda, sur les rives du fleuve Orange.

[…]

Chapitre VI – Où l'on achève de se connaître

[…] Vers la fin de la journée, toute la troupe atteignit une de ces stations occupées par les fermiers nomades, ces "boors" que la richesse des pâturages fixe pour quelques mois en certains lieux. Le colonel Everest et ses compagnons furent hospitalièrement accueillis par ce colon, un Hollandais, chef d'une nombreuse famille, qui, en retour de ses services, ne voulut accepter aucune espèce de dédommagement. Ce fermier était un de ces hommes courageux, sobres et travailleurs, dont le faible capital, intelligemment employé à l'élevage des bœufs, des vaches et des chèvres, se change bientôt en une fortune. Quand le pâturage est épuisé, le fermier, comme un patriarche des anciens jours, cherche une source nouvelle, des prairies grasses, et reconstitue son campement dans d'autres conditions plus favorables.

Ce fermier indiqua très à propos au colonel Everest une large plaine, située à une distance de quinze milles, vaste étendue de terrain plat qui devait parfaitement convenir à des opérations géodésiques.

Le lendemain 5 mars, la caravane partit dès l'aube. On marcha toute la matinée. Aucun incident n'aurait varié la monotonie de cette promenade, si John Murray n'eût abattu d'une balle, à douze cents mètres, un curieux animal, à museau de bœuf, à longue queue blanche, et dont le front est armé de cornes pointues. C'était un gnou, un bœuf sauvage, qui fit entendre en tombant un gémissement sourd.

Le bushman fut émerveillé à voir la bête, frappée avec une telle précision malgré la distance, tomber morte du coup. Cet animal, haut de cinq pieds environ, fournit à l'ordinaire une notable quantité de chair excellente, si bien que les gnous furent spécialement recommandés aux chasseurs de la caravane.

Vers midi, l'emplacement désigné par le fermier était atteint. C'était une prairie sans limite vers le nord, et dont le sol ne présentait aucune dénivellation. On ne pouvait imaginer un terrain plus favorable à la mesure d'une base. Aussi, le bushman, après avoir examiné l'endroit, revint vers le colonel Everest, et lui dit :

"La plaine demandée, colonel."

Chapitre VII – Une base de triangle

L'opération géodésique qu'allait entreprendre la commission était, on le sait, un travail de triangulation ayant pour but la mesure d'un arc de méridien. Or la mesure d'un ou plusieurs degrés, directement, au moyen de règles métalliques posées bout à bout, serait un travail absolument impraticable, au point de vue de l'exactitude mathématique. Aucun terrain d'ailleurs, en aucun point du globe, ne serait assez uni sur un espace de plusieurs centaines de lieues, pour se prêter efficacement à l'exécution d'une opération aussi délicate. Fort heureusement, on peut procéder d'une façon plus rigoureuse, en partageant tout le terrain que doit traverser la ligne du méridien en un certain nombre de triangles "aériens", dont la détermination est relativement peu difficile.

Ces triangles s'obtiennent en visant au moyen d'instruments précis, le théodolite ou le cercle répétiteur, des signaux naturels ou artificiels, tels que clochers, tours, réverbères, poteaux. A chaque signal aboutit un triangle, dont les angles sont donnés par les instruments susdits avec une précision mathématique. En effet, un objet quelconque, - un clocher, le jour, un réverbère, la nuit, - peuvent être relevés avec une exactitude parfaite par un bon observateur qui les vise au moyen d'une lunette dont le champ est divisé par des fils d'un réticule. On obtient ainsi des triangles, dont les côtés mesurent souvent plusieurs milles de longueur. C'est de cette façon qu'Arago a joint la côte de Valence en Espagne aux îles Baléares par un immense triangle, dont l'un des côtés a quatre-vingt-deux mille cinq cent cinquante-cinq toises de longueur (soit 160 kilomètres ou 40 lieues).

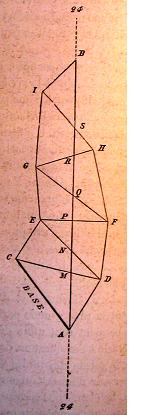Or, d'après un principe de géométrie, un triangle quelconque est entièrement "connu", quand on connaît un de ses côtés et deux de ses angles, car on peut conclure immédiatement la valeur du troisième angle et la longueur des deux autres côtés. Donc en prenant pour base d'un nouveau triangle un côté des triangles déjà formés, et en mesurant les angles adjacents à cette base, on établira ainsi de nouveaux triangles qui seront successivement menés jusqu'à la limite de l'arc à mesurer. On a donc, par cette méthode, les longueurs de toutes les droites comprises dans le réseau de triangles, et par une série de calculs trigonométriques, on peut facilement déterminer la grandeur de l'arc du méridien qui traverse le réseau entre les deux stations terminales.

Il vient d'être dit qu'un triangle est entièrement connu, quand on connaît un de ses côtés et deux de ses angles. Or, ses angles on peut les obtenir exactement au moyen du théodolite ou du cercle répétiteur. Mais ce premier côté, - base de tout le système, - il faut d'abord "le mesurer directement au sol," avec une précision extraordinaire, et c'est là le travail le plus délicat de toute triangulation.

Lorsque Delambre et Méchain mesurèrent la méridienne de France depuis Dunkerque jusqu'à Barcelone, ils prirent pour base de leur triangulation une direction rectiligne sur la route qui va de Melun à Lieusaint, dans le département de Seine-et-Marne. Cette base avait douze mille cent cinquante mètres, et il ne fallut pas moins de quarante cinq jours pour la mesurer. Quels moyens ces savants employèrent-ils pour obtenir une exactitude mathématique, c'est ce qu'apprendra l'opération du colonel Everest et de Mathieu Strux, qui agirent comme avaient agi les deux astronomes français. On verra jusqu'à quel point la précision devait être portée.

Ce fut pendant cette journée du 5 mars que les premiers travaux géodésiques commencèrent au grand étonnement des Bochjesmen, qui n'y pouvaient rien comprendre. Mesurer la terre avec des règles longues de six pieds, placées bout à bout, cela paraissait au chasseur une plaisanterie de savants. En tout cas, il avait rempli son devoir. On lui avait demandé une plaine bien unie, et il avait fourni la plaine.

L'emplacement était bien choisi, en effet, pour la mesure directe d'une base. La plaine, revêtue d'un petit gazon sec et gras, s'étendait jusqu'aux limites de l'horizon suivant un plan nettement nivelé. Certainement les opérateurs de la route de Melun n'avaient pas été aussi favorisés. En arrière ondulait une ligne de collines qui formait l'extrémité sud du Kalahari. Au nord, l'infini. Vers l'est mourraient en pentes douces les versants de ces hauteurs qui composaient le plateau de Lattakou.

[…]

Le 6 mars, les opérations géodésiques commencèrent. Les deux plus jeunes savants de la commission furent chargés des travaux préliminaires.

"En route, mon camarade, dit joyeusement Michel Zorn à William Emery, et que le Dieu de la précision nous soit en aide ! "

La première opération consista à tracer sur le terrain, dans sa partie la plus plate et la plus unie, une direction rectiligne. La disposition du sol donna à cette droite l'orientation du sud-est au nord-ouest. Sa rectitude fut obtenue au moyen de piquets plantés en terre à une courte distance l'un de l'autre, et qui formèrent autant de jalons. Michel Zorn, muni d'une lunette à réticule, vérifiait la pose de ces jalons et la reconnaissait exacte, lorsque le fil vertical du réticule partageait toutes leurs images focales en parties égales.

Cette direction rectiligne fut ainsi relevée pendant neuf milles environ, longueur présumée que les astronomes comptaient donner à leur base. Chaque piquet avait été muni à son sommet d'une mire qui devait faciliter le placement des règles métalliques. Ce travail demanda quelques jours pour être mené à bonne fin. Les deux jeunes gens l'accomplirent avec une scrupuleuse exactitude.

Il s'agissait alors de poser bout à bout les règles destinées à mesurer directement la base du premier triangle, opération qui peut paraître fort simple, mais qui demande, au contraire, des précautions infinies, et de laquelle dépend en grande partie le succès d'une triangulation.

Voici quelles furent les dispositions prises pour le placement des règles en question, qui vont être écrites plus bas.

Pendant la matinée du 10 mars, des socles de bois furent établis sur le sol, suivant la direction rectiligne déjà relevée. Ces socles, au nombre de douze, reposaient par leur partie inférieure sur trois vis de fer, dont le jeu n'était que de quelques pouces, qui les empêchaient de glisser et les maintenaient par leur adhérence dans une position invariable.

Sur ces socles, on disposa de petites pièces de bois parfaitement dressées, qui devaient supporter les règles, et les contenir dans de petites montures. Ces montures en fixaient la direction, sans gêner leur dilatation qui devait varier suivant la température et dont il importait de tenir compte dans l'opération.

Lorsque les douze socles eurent été fixés et recouverts de pièces de bois, le colonel Everest et Mathieu Strux s'occupèrent de la pose si délicate des règles, opération à laquelle prirent part les deux jeunes gens. Quant à Nicolas Palander, le crayon à la main, il était prêt à noter sur un double registre les chiffres qui lui seraient transmis.

Les règles employées étaient au nombre de six, et d'une longueur déterminée d'avance avec une précision absolue. Elles avaient été comparées à l'ancienne toise française, généralement adoptée pour les mesures géodésiques.

Ces règles étaient longues de deux toises, larges de six lignes sur une épaisseur d'une ligne. Le métal employé dans leur fabrication avait été le platine, métal inaltérable à l'air dans les circonstances habituelles, et complètement inoxydable, soit à froid, soit à chaud. Mais ces règles de platine devaient subir un allongement ou une diminution dont il fallait tenir compte, sous l'action variable de la température. On avait donc imaginé de les pourvoir chacune de leur propre thermomètre, - thermomètre métallique fondé sur la propriété qu'ont les métaux de se modifier inégalement sous l'influence de la chaleur. C'est pourquoi chacune de ces règles était recouvertes, d'une autre règle en cuivre, un peu inférieure en longueur. Un vernier, disposé à l'extrémité de la règle en cuivre, indiquait exactement l'allongement relatif de ladite règle, ce qui permettait de déduire l'allongement absolu du platine. De plus, les variations du vernier avaient été calculées de telle sorte, que l'on pouvait évaluer une dilatation, si petite qu'elle fût, dans la règle de platine. Ce vernier était d'ailleurs muni d'un microscope qui permettait d'estimer des quarts de cent millième de toise.

Les règles furent donc disposées sur les pièces de bois, bout à bout, mais sans se toucher, car il fallait éviter le choc si léger qu'il fût, qui eût résulté d'un contact direct. Le colonel Everest et Mathieu Strux placèrent eux-mêmes la première règle sur la pièce de bois, dans la direction de la base. A cent toises de là, environ, au-dessus du premier piquet, on avait établi une mire, et comme les règles étaient armées de deux pointes verticales de fer implantées sur l'axe même, il devenait facile de les placer exactement dans la direction voulue. En effet, Emery et Zorn, s'étant portés en arrière, et se couchant sur le sol, examinèrent si les deux pointes de fer se projetaient bien sur le milieu de la mire. Cela fait, la bonne direction de la règle était assurée.

[…]

"Nous n'avons pas la prétention, je pense, dit le colonel Everest, de placer cette règle dans une position parfaitement horizontale ?

– Non, répondit Mathieu Strux, il suffira de relever avec un niveau l'angle que chaque règle fera avec l'horizon, et nous pourrons ainsi réduire la longueur mesurée avec la longueur véritable."

Les deux savants étant d'accord, on procéda à ce relèvement au moyen d'un niveau spécialement construit à cet effet, formé d'une alidade mobile autour d'une charnière placée au sommet d'une équerre en bois. Un vernier indiquait l'inclinaison par coïncidence de ses divisions avec celles d'une règle fixe portant un arc de dix degrés, divisés de cinq minutes en cinq minutes.

[…]

Il ne restait donc plus qu'à mesurer l'intervalle laissé entre les deux règles. A l'extrémité de la première, et dans la partie qui ne recouvrait point la règle de cuivre, se trouvait une petite languette de platine qui glissait à léger frottement entre deux coulisses. Le colonel Everest poussa cette languette, de manière à ce qu'elle vînt toucher la seconde règle. Comme ladite languette était divisée en dix millièmes de toises, et qu'un vernier inscrit sur une des coulisses et muni de son microscope donnait des cent millièmes, on put évaluer avec une certitude mathématique l'intervalle laissé à dessein entre les deux règles. Le chiffre fut aussitôt porté sur le double registre et immédiatement collationné.

[…]

Telles furent les opérations qui furent conduites avec cette patience et cette minutie pendant plus d'un mois. […]

Bref, l'opération fut menée à bien et conduite avec une extrême précision. Quant à la rigueur mathématique, on devait la contrôler plus tard, en mesurant une nouvelle base à l'extrémité septentrionale de la méridienne.

En somme, cette base, directement mesurée, donna comme résultat huit mille trente-sept toises et soixante-quinze centièmes, et sur laquelle allait s'appuyer la série des triangles dont le réseau devait couvrir l'Afrique australe sur un espace de plusieurs degrés.

Chapitre VIII – Le vingt-quatrième méridien

La mesure de la base avait demandé un travail de trente-huit jours. Commencée le 6 mars, elle ne fut terminée que le 13 avril. Sans perdre un instant, les chefs de l'expédition résolurent d'entreprendre immédiatement la série des triangles.

Tout d'abord, il s'agit de relever la latitude du point sud auquel commençait l'arc de méridien qu'il s'agissait de mesurer. Pareille opération devait être renouvelée au point terminal de l'arc dans le nord, et par la différence des latitudes on devait connaître le nombre de degrés de l'arc mesuré.

Dès le 14 avril, les observations les plus précises furent faites dans le but de déterminer la latitude du lieu. Déjà, pendant les nuits précédentes, lorsque l'opération de la base était suspendue, William Emery et Michel Zorn avaient obtenu de nombreuses hauteurs d'étoiles au moyen d'un cercle répétiteur de Fortin. Ces jeunes gens avaient observé avec une précision telle, que la limite des écarts extrêmes des observations ne fut même pas de deux secondes sexagésimales, écarts dus probablement aux variétés des réfractions produites par les changements de figure des couches atmosphériques.

De ces observations si minutieusement répétées, on put déduire avec une approximation plus que suffisante la latitude du point austral de l'arc.

Cette latitude était, en degrés décimaux, de 27,951789.

La latitude ayant été ainsi obtenue, on calcula la longitude, et le point fut reporté sur une excellente carte de l'Afrique australe, établie sur une grande échelle. Cette carte reproduisait les découvertes géographiques faites récemment dans cette partie du continent africain, les routes des voyageurs et naturalistes, tels que Livingstone, Anderson, Magyar, Baldwin, Vaillant, Burchell, Lichtenstein. […]

Après discussion, on reconnut que l'extrémité sud de la base pouvait servir de point de départ. Ce méridien était le vingt-quatrième à l'est de Greenwich : il se prolongeait sur un espace d'au moins sept degrés, du vingtième au vingt-septième sans rencontrer d'obstacles naturels, ou tout au moins, la carte n'en signalait aucun. Vers le nord seulement, il traversait le lac Ngami dans sa portion orientale, mais ce n'était point là un empêchement insurmontable, et Arago avait éprouvé des difficultés bien autrement grandes, lorsqu'il joignit géodésiquement la côte d'Espagne aux îles Baléares.

Il fut donc décidé que l'arc à mesurer serait pris sur le vingt-quatrième méridien, qui, prolongé en Europe, donnerait la facilité de mesurer un arc septentrional sur le territoire même de l'empire russe.

Les opérations commencèrent aussitôt, et les astronomes s'occupèrent de choisir la station à laquelle devait aboutir le sommet du premier triangle, qui aurait pour base la base mesurée directement.

La première station fut choisie vers la droite de la méridienne. C'était un arbre isolé, situé à une distance de dix milles environ, sur une extumescence du sol. Il était parfaitement visible, et de l'extrémité sud-est de la base et de son extrémité nord-ouest, points auxquels le colonel Everest fit élever deux pylônes. Son sommet effilé permettait de le relever avec une extrême précision.

Les astronomes s'occupèrent d'abord de mesurer l'angle que faisait cet arbre avec l'extrémité sud-est de la base. Cet angle fut mesuré au moyen d'un cercle répétiteur de Borda, disposé pour les observations géodésiques. Les deux lunettes de l'instrument étaient placées de telle façon que leurs axes optiques fussent exactement dans le plan du cercle ; l'une visait l'extrémité nord-ouest de la base, et de l'autre, l'arbre isolé choisi dans le nord-est ; elles indiquaient ainsi par leur écartement, la distance angulaire qui séparait ces deux stations. Inutile d'ajouter que cet admirable instrument, construit avec une extrême perfection, permettait aux observateurs de diminuer autant qu'ils le voulaient les erreurs d'observation. Et en effet, par la méthode de la répétition, ces erreurs, quand les répétitions sont nombreuses, tendent à se compenser et à se détruire mutuellement. Quant aux verniers, aux niveaux, aux fils à plombs destinés à assurer la pose régulière de l'appareil, ils ne laissaient rien à désirer. La commission anglo-russe possédait quatre cercles répétiteurs. Deux devaient servir aux opérations géodésiques, tels que le relèvement des angles qui devaient être mesurés ; les deux autres, dont les cercles étaient placés dans une position verticale, permettaient, au moyen d'horizons artificiels, d'obtenir des distances zénithales, et par conséquent de calculer, même dans une seule nuit, la latitude d'une station avec l'approximation d'une petite fraction de seconde. En effet, dans cette grande opération de triangulation, il fallait non seulement obtenir la valeur des angles qui formaient les triangles géodésiques, mais aussi mesurer à de certains intervalles la hauteur méridienne des étoiles, hauteur égale à la latitude de chaque station.

[…]

Chapitre XI – Où l'on retrouve Nicolas Palander

[…]

"Le voilà ! le voilà ! " s'écria le bushman.

En effet, à l'extrémité d'une sorte de presqu'île, assis sur une souche, immobile, à trois cents pas de distance, Nicolas Palander était là, ne voyant rien, n'entendant rien, un crayon à la main, un carnet placé sur ses genoux, calculant sans doute !

Ses compagnons ne purent retenir un cri. Le savant russe était guetté, à vingt pas au plus, par une bande de crocodiles, la tête hors de l'eau, dont il ne soupçonnait même pas la présence. Ces voraces animaux avançaient peu à peu, et pouvaient l'enlever en un clin d'œil.

"Hâtons nous ! dit le chasseur à voix basse, je ne sais ce que les crocodiles attendent pour se jeter sur lui !

– Ils attendent peut-être qu'il soit faisandé !" ne put s'empêcher de répondre sir John, faisant allusion à ce fait observé par les indigènes, que ces reptiles ne se repaissent jamais de viande fraîche.

Le bushman et sir John recommandèrent à leurs compagnons de les attendre en cet endroit, et ils tournèrent le lagon de manière à gagner l'isthme étroit qui devait les conduire près de Nicolas Palander.

Ils n'avaient pas fait deux cents pas, quand les crocodiles, quittant les profondeurs de l'eau, commencèrent à ramper sur le sol, marchant droit à leur proie.

Le savant ne voyait rien. Ses yeux ne quittaient pas son carnet. Sa main traçait encore des chiffres.

"Du coup d'œil, du sang-froid, ou il est perdu ! " murmura le chasseur à l'oreille de sir John.

Tous deux, alors, mirent genoux à terre, et visant les reptiles les plus rapprochés, ils firent feu. Une double détonation retentit. Deux des monstres, l'épine dorsale brisée, culbutèrent dans l'eau, et le reste de la bande disparut en un instant sous la surface du lac.

Au bruit des armes à feu, Nicolas Palander avait enfin relevé la tête. Il reconnut ses compagnons, et courant vers eux, en agitant son carnet :

"J'ai trouvé ! j'ai trouvé ! s'écriait-il.

– Et qu'avez-vous trouvé, monsieur Palander ? lui demanda sir John.

– Une erreur de décimale dans le cent troisième logarithme de la table de James Wolston ! "

En effet, il avait trouvé cette erreur, le digne homme ! Il avait découvert une erreur de logarithme ! Il avait droit à la prime de cent livres promise par l'éditeur James Wolton ! Et, depuis quatre jours qu'il errait dans ces solitudes, voilà à quoi avait passé son temps le célèbre astronome de l'observatoire d'Helsingfors !

[…]

Chapitre XIX – Trianguler ou mourir

[…]

"Messieurs, dit-il, l'opération sera difficile, minutieuse, elle demandera de la patience et du zèle, mais elle n'est point impraticable. De quoi s'agit-il ? De relier géodésiquement le Scorzef avec une station située au nord du lac ? Or, cette station existe-t-elle ? Oui, elle existe, et j'avais déjà choisi à l'horizon un pic qui pût servir de mire à nos lunettes. Il s'élève dans le nord-ouest du lac, de telle sorte que ce côté du triangle coupera le Ngami suivant une ligne oblique.

– Et bien, dit le colonel Everest, si le point de mire existe, où est la difficulté ?

– La difficulté, répondit Mathieu Strux, sera dans la distance qui sépare le Scorzef de ce pic !

– Quelle est donc cette distance ? demanda le colonel Everest.

– Cent vingt milles au moins.

– Notre lunette la franchira.

– Mais il faudra allumer un fanal au sommet de ce pic.

– On l'allumera.

– Il faudra l'y porter ?

– On l'y portera.

– Et pendant ce temps, se défendre contre les Makololos ! ajouta le bushman.

– On se défendra !

– Messieurs, dit le bushman, je suis à vos ordres, et je ferai ce que vous me commanderez de faire ! …"

[…]

Chapitre XXI - Fiat lux !

[…]

Tous devaient fuir ou demeurer ensemble. Quant à abandonner le Scorzef avant d'avoir terminer l'opération géodésique, il n'en fut même pas question. On devait attendre, tant que toutes les chances de réussite n'auraient pas été épuisées. C'était une affaire de patience ! On serait patient !

"Lorsque Arago, Biot et Rodrigues, dit ce jour là le colonel Everest à ses compagnons rassemblés autour de lui, se proposèrent de prolonger la méridienne de Dunkerque jusqu'à l'île d'Iviça, ces savants se trouvèrent à peu près dans la situation où nous sommes. Il s'agissait de rattacher l'île à la côte d'Espagne par un triangle dont les côtés dépasseraient cent vingt milles. L'astronome Rodrigues s'installa sur des pics de l'île, et y entretint des lampes allumées, tandis que les savants français vivaient sous la tente, à plus de cent milles de là, au milieu du désert de las Palmas. Pendant soixante nuits, Arago et Biot épièrent le fanal dont ils voulaient relever la direction ! Découragés, ils allaient renoncer à leur observation, quand, dans la soixante et unième nuit, un point lumineux que son immobilité seule ne permettait pas de confondre avec une étoile de sixième grandeur, apparut dans le champ de leur lunette. Soixante et une nuits d'attente ! Et bien, messieurs, ce que deux astronomes français ont fait dans un grand intérêt scientifique, des astronomes anglais et russes ne peuvent-ils le faire ? "

[…]

La mitrailleuse ne pouvait plus suffire à atteindre les indigènes qui se présentaient en foule devant toutes les brèches, en poussant leurs cris de mort. Ce fut dans ces conditions, et devant ces ouvertures défendues pied à pied, que le combat continua pendant une demi-heure encore. Les assiégés, protégés par leurs armes à feu, n'avaient reçu que des égratignures dues à quelques pointes d'assagaies. L'acharnement ne diminuait pas de part et d'autre, et la colère grandissait au milieu de ces engagements corps à corps.

Ce fut alors, vers onze heures et demie, au plus épais de la mêlée, au milieu des fracas de la fusillade, que Mathieu Strux apparut près du colonel Everest. Son œil était à la fois rayonnant et effaré. Une flèche venait de percer son chapeau et tremblotait encore au-dessus de sa tête.

"Le fanal ! le fanal ! s'écria-t-il.

– Hein ! répondit le colonel Everest, en achevant de charger son fusil.

– Oui ! le fanal !

– Vous l'avez vu ?

– Oui !"

Cela dit, le colonel déchargea une dernière fois son rifle, poussa un hurrah de triomphe, et se précipita vers le donjon, suivi de son intrépide collègue.

Là, le colonel s'agenouilla devant la lunette, et, comprimant les battements de son cœur, il regarda. Ah ! comme en ce moment toute sa vie passa dans son regard ! Oui ! le fanal était là, étincelant entre les fils du réticule ! Oui ! la lumière brillait au sommet du Volquiria ! Oui ! le dernier triangle venait enfin de trouver son point d'appui.

C'eut été vraiment un spectacle merveilleux que de voir opérer les deux savants pendant le tumulte du combat. Les indigènes, trop nombreux, avaient forcé l'enceinte. Sir John, le bushman, leur disputaient le terrain pas à pas. Aux balles répondaient les flèches des Makololos, aux coups d'assagaies, les coups de hache. Et cependant, l'un après l'autre, le colonel Everest et Mathieu Strux, courbés sur leur appareil, observaient sans cesse ! Ils multipliaient les répétitions du cercle pour corriger les erreurs de lectures, et l'impassible Nicolas Palander notait sur son registre les résultats de leurs observations ! Plus d'une fois, une flèche leur rasa la tête, et se brisa sur le mur intérieur du donjon. Ils visaient toujours le fanal du Volquiria, puis ils contrôlaient à la loupe les indications du vernier, et l'un vérifiait sans cesse le résultat obtenu par l'autre !

"Encore une observation," disait Mathieu Strux, en faisant glisser les lunettes sur le limbe gradué.

Enfin, une énorme pierre lancée par la main d'un indigène, fit voler le registre des mains de Palander, et, renversant le cercle répétiteur, le brisa.

Mais les observations étaient terminées ! La direction du fanal était calculée avec une approximation d'un millième de seconde !

Maintenant il fallait fuir, sauver le résultat de ces glorieux et magnifiques travaux. […]

Chapitre XXIII- Les chutes du Zambèse

[…] la petite troupe, arrivée non loin des chutes du Zambèse, rencontra une plaine qui s'étendait sur une largeur de plusieurs milles. Le terrain convenait parfaitement à la mesure directe d'une base. […]

Lorsque les longueurs obtenues eurent été réduites par les calculateurs en arcs rapportés au niveau moyen de la mer, et à la température de soixante et un degrés du thermomètre de Fahrenheit (16°11' centigrades), Nicolas Palander et William Emery présentèrent à leurs collègues les nombres suivants :

Base nouvelle mesurée : ……… 5075 t,25

Avec la même base déduite de la première base et du réseau

trigonométrique tout entier : ….. 5075 ,11

Différence entre le calcul et l'observation : …. 0 t,14 .

[…]

Un triple hurrah salua ce résultat admirable, sans précédent dans les annales scientifiques !

[…]

Les opérations géodésiques étaient donc entièrement terminées. Les astronomes avaient achevé leur tâche. Il ne leur restait plus qu'à gagner les bouches du Zambèse, en suivant, en sens inverse, l'itinéraire que devait parcourir le docteur Livingstone dans son second voyage de 1858 à 1864.

Pour revenir à la page "Triangulation", cliquer sur bouton Précédente de votre navigateur ou sur le lien :

Retour à la page Triangulation