Livre 3
DES HORLOGES ET QUADRANTS SOLAIRES
D’ORONCE FINE DU DAUPHINE
Traduit de l’italien par Marie-Agnès Pédaillé.

Des horloges et
quadrants solaires
d’Oronce Finé du
Dauphiné
Livre Trois
———
Du Quadrant Universel.
Chap. I

l me plait finalement d'expliquer dans ces deux derniers
livres [livres 3 et 4 des horloges solaires] le quadrant universel,
explication que j'avais promise plusieurs fois, tirée de la composition du
Planisphère de Ptolémée, et de celle de l'Astrolabe. Dans le premier livre
j'exposerai la manière de faire, et dans le dernier les grands avantages et
particularités dudit instrument.
La première image, qui nous vient de ce quadrant, nous a été offerte par l'astrolabe. J'ai dessiné sur un papier très fin l'astrolabe en question, avec l'écliptique, et plusieurs divers horizons, distribués avec cet intervalle qui m'a paru le plus pertinent [en fait tous les 5°], mais sans y représenter les cercles verticaux ni ceux des latitudes [cercles d'azimut et de hauteur].
Puis j'ai plié l'autre moitié dudit astrolabe à droite de
la ligne méridienne et de nouveau sur la pliure qui correspondait à ce moment à
la moitié de l'astrolabe, j'ai replié sur l'horizon droit [perpendiculaire au
méridien menée par le centre] pour en avoir le quart ; et de cette manière j'ai
réduit en quatre ledit dessin de l'astrolabe. Des lignes duquel j'ai tiré la
première constatation que j'ai faite à propos des lignes, à savoir des arcs qui
convergent, grâce à la transparence et à la très fine épaisseur de ce papier,
puis j'ai voulu communiquer ces lignes [les tracés] à tous ceux qui
étudient cet art qui suit.
Donc pour faire cette chose de la manière la plus
heureuse possible, dessine sur une surface plane de n’importe quelle matière
que tu auras choisie, prépare à partir du centre A un cercle, qui soit BCDE,
qui représente le tropique du Cancer [erreur du texte : il s’agit du
tropique du Capricorne], tu le diviseras en quatre quarts avec les diamètres
BD et CE qui se coupent au point A à angle droit. Ensuite divise le quadrant BE
en 90 parties égales : et tu obtiendras du point E vers le point B la plus
grande déclinaison du Soleil, laquelle soit EF [l’angle EAF mesure
23°1/2], et tire à partir de F à D [le point D est sur le tropique du
Capricorne à gauche du dessin] une ligne sans encre qui soit DE, et qui
coupe AE au point G [en dessous de E].
Et à partir du centre A, jusqu’à obtenir l’intervalle AG, dessine le cercle
GHIK, lequel cercle sert pour l’Equinoxial [c’est à dire l’Equateur].
Puis tire une ligne depuis le centre A au point F, qui soit AF, qui divise le
quart ou quadrant de l’Equinoxial GH au point L, duquel tu tireras une ligne
droite jusqu’en K, qui soit le trait fin KL, qui coupe le demi-diamètre AE au
point M. Et de nouveau à partir de A, tu dessineras à la mesure de AM, le
tropique du Capricorne MNOP [il s’agit en fait du tropique du Cancer, comme
l’indique la figure ; à partir de là chacun des trois cercles susdits
sera divisé en quatre quarts de diamètres BD et CE : desquels vers la droite
sur ABC, nous choisirons de faire [le Quadrant Universel], comme étant
le plus commode.
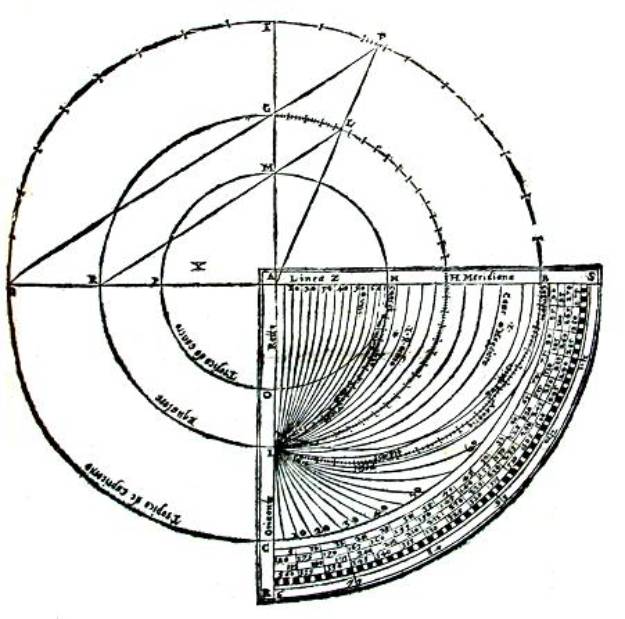
Comment on distribue le
limbe de ce quadrant,
c’est à dire en combien de
parties.
Chap. II

l faut ensuite dessiner sur ce quadrant BC un certain
limbe [partie sur le bord circulaire du quadrant], dans lequel sont les
divisions des degrés, et également celles des heures, et également encore les
nombres qui correspondent à l’Equinoxial [l’Equateur]. A partir de là il
faut étendre les demi-diamètres AB, et AC, droitement, et tout au long, jusqu’à
R et S, et autour du centre A sont tracés sept arcs parallèles sur le quadrant
BC, qui forment avec ledit BC sept intervalles, et le dernier d’entre eux soit
RS [il s’agit des couronnes extérieures du quadrant qui vont être graduées].
Dans le dernier intervalle, et le plus grand de tous, tu compartimenteras six
intervalles pour les heures avec des lignes droites qui vont du premier arc BC
jusqu’à RS, à partir du centre A. Et les nombres de ces heures [seront]
ordonnés dans cet intervalle de telle manière que l’une et l’autre heure 6 [6
heures et 18 heures] vienne sur R, et la 12 sur S. De manière à ce que ces
divisions des douze heures servent ainsi à celles d’avant midi, comme à celles
d’après midi. Tu diviseras ensuite chacune des 6 parties en 3 parties égales,
et tu tireras les lignes droites seulement pour 5 intervalles des dits arcs
[on ne gradue que cinq arcs], et cela te donneras 18 parts, chacune d’entre
elles servira pour 5 degrés, desquels tout le quadrant RS est 90. Redivise de
nouveau celle qui est la première des 18 parts en 5 et tire de nouveau les
petites lignes seulement du cinquième au sixième intervalle [cases
alternativement noires et blanches], et tu auras 90 parties lesquelles
multipliées par quatre te représenteront l’Equinoxial entièrement. Il faut
ensuite écrire les numéros des degrés dans les quatre intervalles dans leurs
petits espaces de cinq en cinq, en laissant le premier intervalle vide ;
et puis tu commenceras le second après BC à partir de la gauche à 5 et suivra
jusqu’à 90 et en retournant l’autre intervalle, tu suivras 95, 100 et ainsi tu
auras suivi successivement de telle manière que lorsque tu auras terminé le
travail sur chacun des quatre intervalles et leurs petits espaces en suivant
cet ordre, tu arriveras jusqu’au dernier au numéro 360 comme te montre la
figure.
Comment on dessine les arcs
horizontaux,
comme le veut l’élévation du
pôle.
Chap. III

a première chose que tu dois savoir, c’est que le
demi-diamètre AG (comme il intervient dans l’astrolabe) sert ou représente
l’horizon droit [il s’agit de l’horizon d’un observateur situé à
l’équateur, qui passe par les pôles, et est le seul à être projeté selon une
droite]. Mais les horizons circulaires, tu les dessineras selon les climats [c’est
à dire selon les latitudes], en les distribuant également selon ce que tu
voudras comme intervalles de degrés [Finé choisira de les tracer tous les
5° de latitude], de cette manière. Divise comme il faut le quart de
l’Equinoxial en 90 parts égales, avec des petites lignes très fines, et tu
auras ensuite sur ledit horizon ta hauteur du pôle [la latitude], dans
le quadrant de l’Equinoxial HI, du point I vers H ; et pose la règle au
terme nouvellement obtenu, et en G[on compte sur l’arc d’équateur à partir
de I vers H un angle égal à la latitude et on relie le point obtenu au point G],
et fait un point où ladite règle coupe la ligne méridienne AB, et fait la même
chose dans le quadrant GK, de G jusqu’à K, en notant de nouveau l’intersection
que fait ladite règle avec l’autre partie du méridien AD, allongée droitement
autant que l’on veut [on compte à partir de G sur l’arc d’équateur GK un
angle égal à la latitude et on relie le point obtenu au point G puis on cherche
l’intersection avec la ligné méridienne prolongée], et la longueur, qui est
comprise entre ces deux points, divise là en deux, de telle manière que ce
point sera le centre de la partie boréale de cet horizon.
A partir de là un pied des sixtes [il s’agit sans
doute d’un pied d’un compas à deux branches de 6 pouces] est fixé, et ouvre
l’autre jusqu’au point de AB, ou point I, dessine et tire l’arc boréal de cet
horizon du point I jusqu’à la Méridienne AB : de sorte qu’il doive passer
par ces deux points et par le point G pour que tu ne te sois pas trompé [le
cercle centré sur le milieu des points d’intersection obtenus sur la méridienne
et mené par I, passe par G et donne la partie nord de l’horizon]. Puis sans
bouger le sixte [l’écartement du compas], pose de nouveau un pied au
point I, et l’autre sur la Méridienne AB ; et tire la partie méridionale
dudit horizon à partir du même point I, qui indique l’intersection commune des
horizons avec l’Equinoxial, incliné vers le Tropique BC du Capricorne. De sorte
que, le centre de la partie australe dudit horizon sera autant éloigné du point
A vers B, que le centre de la partie boréale l’est de A vers D [autrement
dit, prendre le symétrique par rapport à A du centre de l’arc de l’horizon
nord, y planter le compas avec le même écartement, et tracer entre I et le
tropique du Capricorne la partie sud de l’horizon]. Ainsi que tu peux en
faire l’expérience grâce à l’horizon sur lequel le pôle arctique s’élève à 45
degrés, duquel le centre est appelé K et le centre de la partie australe
H ; et de même pour les autres, en distribuant sur cette figure les degrés
de 5 en 5 ; auxquels degrés du pôle il m’est apparu de donner des noms
pour une meilleure déclaration de toutes les choses dites.

Comment on peut diviser la
ligne méridienne
de manière proportionnelle
et la transformer en un
index mobile.
Chap. IIII

l faut à partir de là diviser la ligne Méridienne AB en
parts, mais non égales, mais proportionnellement à l’astrolabe [c’est à
dire selon la projection stéréographique].De là tu poseras la règle au point
G, et chaque partie de la moitié de l’Equinoxial GHI, depuis le point I jusqu’à
A [on relie le point G à chaque graduation tous les 5° de l’arc d’équateur
IHG] ; et tu seras attentif à toutes les intersections, que fait la
règle sur la Méridienne AB. Puis tu feras un index selon une demi-ligne [un
rayon] de l’astrolabe, comme TV [lettres désignant respectivement le point de rotation de l’index et la
graduation 0 de l’index], long autant que la moitié du diamètre du quadrant
ARS. Et depuis la tête de cet index jusqu’au centre tu reporteras sur la ligne
de foi toutes les divisions préparées sur AB et tu les diviseras avec leurs
propres petites lignes et espaces, en y reportant pour l’usage des nombres,
comme tu pourras le voir sur la figure qui suit. Cet index pose le sur le
centre A de telle manière que ladite ligne de foi posée à droite dudit centre
puisse librement aller de gauche à droite, que chacune des divisions de ladite
règle corresponde aux divisions de la Méridienne AB.

Comment on doit dessiner
l’écliptique,
ou le zodiaque avec les
douze signes,
et avec leurs parties ou
degrés.
Chap. V

l est nécessaire de dessiner ensuite les deux parties de
l’Ecliptique ou zodiaque, inclinées vers le Boréal ou vers l’Austral, c’est à
dire le Nord et le Sud, qui se déplacent de l’Equinoxial aux Tropiques. De là
tu diviseras la droite DN en deux parties au point X [les points D et N
correspondent aux solstices] et d’autant que représente l’intervalle XN tu
dessineras la partie boréale de l’Ecliptique qui soit IN [arc de cercle de
centre X] et de nouveau d’autant
que sera AX tu feras AZ et à partir du centre Z sans bouger le sixte
[compas] dessine la partie australe du même Ecliptique qui soit BI [le
centre Z est le symétrique de X par rapport à A et le rayon est le même]. De nouveau tu dessineras deux parallèles
à ces deux parties de l’Ecliptique qui soient également éloignés dudit
Ecliptique sur lesquelles il faut mettre les divisions et les noms des signes.
Il faut ensuite diviser l’une et l’autre moitié de
l’Ecliptique en l’une de ces deux manières en signes et en parties des mêmes
signes (ces manières c’est moi qui les ai choisies comme étant les plus fidèles
de toutes). La première c’est en se servant des ascensions droites des trois
premiers signes. La seconde se sert du pôle de l’Ecliptique. Nous avons de là
rassemblé pour plus de brièveté les ascensions droites du Bélier, du Taureau,
et des Gémeaux, traités dans le troisième chapitre du troisième livre de ma
Cosmographie qui traite de cette affaire que nous avons réduite dans la table
qui suit et que j’ai adaptée aux autres signes.
De là tu obtiendras dans le quadrant RS l’ascension
droite des 5 premiers degrés du Bélier et en ayant posé la règle au degré de
cette ascension [sur la graduation en degrés du limbe] et au centre A tu
noteras les intersections que fera ladite règle avec l’une et l’autre partie de
ladite Ecliptique. Tu observeras la même méthode avec l’ascension droite de 10
degrés et ceux qui suivent jusqu’à la fin des Gémeaux. Tu tireras encore des
petites lignes qui partiront des signes d’un parallèle à l’autre de
l’Ecliptique et tu rediviseras chacune de ces parties de chaque signe en 5
degrés avec des divisions plus fines et finalement tu y reporteras le nom des
signes : les boréaux dans la partie de l’Ecliptique IN et les austraux
dans la partie méridionale BI. Tu les sépareras et avec le même ordre des noms
desdits signes, soit encore avec la différence des caractères comme te le
montre la figure.

Tu pourras encore diviser l’Ecliptique d’une autre
manière, ainsi. Tu obtiendra dans le quadrant GH, du point G jusqu’à H la plus
grande déclinaison du Soleil, et en ayant posé à ce degré la règle [point
L], et au point I, observe où ladite règle coupe la Méridienne AB :
telle celle-c,i et également distante tu en reportera une [longueur] du
centre A jusqu’à D ; et ces divisions formeront les parties du pôle de
l’Ecliptique : à partir de là, et à main gauche, de la partie boréale IN,
et à l’intérieur, et à droite, de la partie australe BI [le point obtenu à
gauche de A est la projection du pôle de l’écliptique, valable pour l’arc IN,
le point symétrique par rapport à A est à prendre comme pôle de l’écliptique
pour l’arc rabattu IB].A partir de là tu poseras la règle au pôle
correspondant à la partie de l’Ecliptique, et à chaque division du quadrant
HI ; et après avoir noté les intersections, que fera ladite règle avec ces
parties de l’Ecliptique et une fois posée de nouveau la règle au centre A, et à
chaque point déjà noté de chaque partie, et qui deux à deux se correspondent,
tire des petites lignes, qui divisent ainsi les signes, autant de degrés dont
tu as l’usage : et puis finis les autres comme je te l’ai dit [cette
partie est peu claire, on doit diviser l’écliptique en mesurant les angles au
pôle de celui-ci, on ne peut donc pas utiliser directement l’échelle de l’arc HI,
l’équateur, un rapporteur centré sur le pôle de l’écliptique semble nécessaire].
Comment il faut reporter les
étoiles sur le quadrant.
Chap. VI

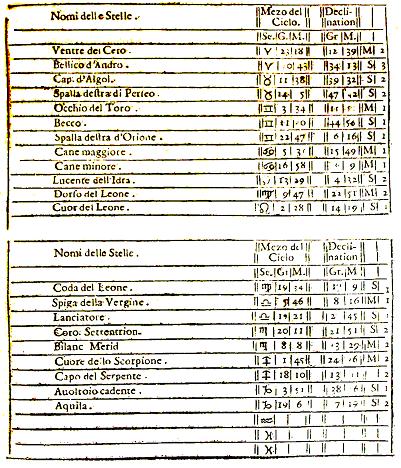
u devras d’abord connaître la déclinaison depuis l’Equinoxial
des plus notables étoiles fixes, de la première et de la deuxième grandeur, et
puis le degré de l’Ecliptique, avec lequel chacune de ces seules dites étoiles
arrive au milieu du Ciel [les étoiles sont repérées par leur déclinaison et
leur longitude céleste], comme tu peux le voir dans la table qui suit,
laquelle, à partir de quoi tu peux faire ledit quadrant (tandis que nous
donnons un fidèle calcul des étoiles), nous avons tirée à partir des calculs et
des observations des modernes.
Quand tu voudras, à partir de là, reporter chacune
desdites étoiles fixes sur le quadrant, étend la ligne de foi de l’index qui
est mobile sur le degré du milieu du Ciel qu’occupe l’étoile noté dans une des
deux parties de l’Ecliptique [autrement dit, sur la graduation de l’écliptique
correspondant à la longitude de l’étoile] et maintenant fermement à cette
place l’index, tu observeras sur ledit index la déclinaison de ladite étoile et
si [la déclinaison est] Boréale à partir de V [graduation 0 sur l’index],
ou Equinoxial, vers le pôle Arctique, ou le centre A du quadrant ; ou vers
le limbe RS, si la déclinaison préalable est Australe.
Ceci fait, marque un point à la fin de cette déclinaison,
lequel représentera le centre de l’étoile étudiée. DE là tu y mettras son nom,
écrit avec des lettres semblables, et depuis cette partie, avec les mêmes
lettres que tu as utilisées, tu nommeras le point du milieu du Ciel étudié [il
s’agit d’indiquer à quel signe de l’écliptique appartient la longitude de l’étoile
et savoir ainsi dans quel quadrant, parmi les quatre, elle se situe, avant leur
pliage sur le quadrant astrolabe] ; comme tu peux le voir sur la figure
avec l’œil du Taureau [a Taurus =
Aldébaran], le Grand Chien [= Sirius] et le Vautour [= Vultur = a Aquila = Altaïr]. Là je pense que tu n’as
plus besoin de mots, la chose est tellement aisée que tu n’as plus besoin d’explication.

Ce qu’il est raisonnable de faire
dans la partie de derrière
dudit quadrant, après ce qui
a été dit.
Chap. VII

u tires finalement ces côtés ou demi-diamètres AR et AS, d’une
distance telle qu’ils soient parallèles suivant la largeur de l’index déjà
utilisé, taille, ou enlève avec une lime toutes les autres choses [on donne
au quadrant sa forme finale]. Puis dans le dos dudit instrument tu
dessineras avec un ordre quasi identique à celui que nous t’avons enseigné dans
le chapitre VIII du livre précédent [le chapitre VIII du livre 2 traite du « quadrant
ancien » dont la gravure est reproduite ci-après] les heures inégales
et l’autre échelle [le « carré des ombres » sans doute], avec
deux mires, percées adroitement diamétralement [les pinnules que l’on
aperçoit en haut de la gravure] et avec le même fil, perle et plomb. Ayant
déjà assez parlé de ces choses dans le susdit huitième chapitre, pour ne pas
multiplier en vain les paroles et pour ne pas causer plus d’ennui que de
plaisir à celui qui le lit uniquement pour comprendre le fonctionnement de ce
quadrant, j’aime donner fin à ce troisième livre, je t’ai mis d’ailleurs avant
tout la figure de toutes les choses dites comme tu pourras le constater [suit
en effet la grande gravure donnée ici au début].

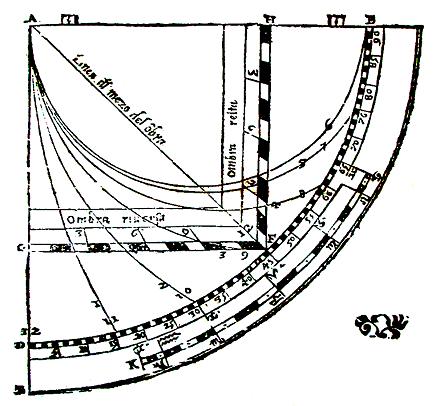
Gravure du « quadrant ancien », donnée au chapitre VIII du livre 2 Des horloges et quadrants solaires :

Suivre les liens :
· Vers la traduction du livre 4
· Vers le descriptif du Quadrant Universel d'Oronce Finé