Trigonométrie
La trigonométrie, essentiellement utilisée en astronomie depuis l’antiquité, s’est au cours des ans constituée en une branche des mathématiques structurée, développant de manière concomitante la trigonométrie plane et la trigonométrie sphérique. A partir du XVIe siècle la trigonométrie s’infiltre dans de nombreux domaines des sciences appliquées, particulièrement en topographie et en navigation. La lourdeur des calculs qu’elle engendre franchit une étape libératrice avec la découverte des logarithmes au début du XVIIe siècle. Avec l’arrivée des calculatrices, la trigonométrie devient facile d'accès. Avec l’arrivée des instruments connectés, sa présence devient particulièrement discrète. Sous-jacente à la modernité, la trigonométrie a une histoire riche…
L’ASSP porte une attention particulière à la trigonométrie contenue dans les manuscrits dont elle mène l’étude. Cet intérêt prend appui sur un travail de plusieurs années mené dans le cadre du « Groupe Trigonométrie » de l’IREM de Rouen, de 2002 à 2007.
- La trigonométrie dans l'Antiquité
- La trigonométrie plane à l’époque moderne
- La trigonométrie à l’Époque contemporaine
- Calcul des lignes trigonométriques
- Notions de trigonométrie sphérique
- La trigonométrie sphérique de Stevin, 1599/1608
- La trigonométrie sphérique de Denoville, 1760
- La Trigonométrie de Levasseur 1610/1626
 Transmission, 1534
|
De la corde grecque au sinus indien La phase arabe de l’histoire de la trigonométrie
En de nombreuses occasions, Ahmed Djebbar est intervenu à l’IREM de Rouen, le creuset de notre association. Ce dernier retrace ici les premiers pas de la trigonométrie. Article publié en 2004 dans les Instruments scientifiques chez Ellipses. |
|
Manesson-Mallet, 1702
|
La trigonométrie de Marolois
Un texte de 1616 concis accompagné d’une analyse claire de chacun des paragraphes, voilà un outil idéal pour commencer l’étude de la trigonométrie. Cette étude qui nous fut particulièrement salutaire, est le fruit du travail de collègues Frédéric Métin et Marie-Noëlle Racine de l’IREM de Dijon. Exploration du fonds ancien de la BMR De 2000 à 2005, le groupe « trigonométrie » de l’IREM de Rouen a exploré le fonds ancien de Bibliothèque municipale de Rouen et analysé les multiples ouvrages de trigonométrie conservés en ce lieu ou à la Bnf. La trigonométrie plane dans l’Occident latin
Publiés en 2004 dans les Instruments scientifiques (Ellipses), différents aspects de la trigonométrie plane à l’époque moderne sont ici présentés par Christian Vassard et Elisabeth Hébert. Sommaire
La trigonométrie dans l’occident latin
La résolution de triangles et ses applications Les instruments au service de la trigonométrie Les tables trigonométriques Quelques compléments
La trigonométrie de Régiomontanus, 1464/1533
La trigonométrie plane en 1760
La diversité des lignes à l’Epoque moderne Les prémices de la trigonométrie du triangle rectangle Rhéticus,1554/1596 et Viète,1571 Les formules usuelles L’étude approfondie du manuscrit de Denoville, conservé à la BM de Rouen, est l’occasion pour Christian Vassard d’expliciter le propre de la trigonométrie plane telle qu’elle est usitée pendant plusieurs siècles… avant que les nombres négatifs ne soient d’usage, et que le rayon du cercle trigonométrique n’adopte la valeur 1. |
 Un précurseur, Euler (1707-1783)
|
Si l’Epoque moderne commence avec l’avènement de la Révolution, il va de soi que la Trigonométrie ne franchit pas, avec ces évènements, un pas décisif, néanmoins elle quitte progressivement l’univers exclusif de la Géométrie pour rentrer dans celui de l’Analyse. Une nouvelle Trigonométrie prend forme. Trigonométrie et Analyse
La formule de Moivre, 1722 L’enseignement de la trigonométrie
Tableau comparatif Evolution des concepts
L’évolution des unités de mesure des angles |
 Tables de Girard, 1672
|
Christian Vassard et Sylvie Colesse, tous deux animateurs à l’IREM de Rouen au sein du groupe Trigonométrie, ont présenté en diverses occasions leurs recherches sur les tables trigonométriques. On trouvera ici :
|
 Tout ce que vous voulez savoir sur la trigonométrie sphérique
Quand des passionnés d’histoire de la trigonométrie rencontrent des passionnés de cadrans solaires et de navigation, la demande d’un approfondissement de la trigonométrie sphérique devient incontournable… De là, l’apport de Catherine Philippe, qui a commis en 2007 pour l’IREM de Rouen, le fascicule Notions de trigonométrie sphérique et exemples d’utlisation. L’intégralité. |
|
|
Triangles sphériques
Intersection d’une sphère et d’un plan
La formule des cosinus |
 |
 |
 |
|
À la charnière des XVIe et XVIIe siècles, le flamand Stevin publie ses recherches dans plusieurs domaines des mathématiques et de la physique naissante. La traduction française de ses travaux paraît dans Œuvres mathématiques de Simon Stevin, revu corrigé et augmenté par Albert Girard en 1634. Intégralité du livre « Des triangles » |
|
 Stevin revu par girard en 1634
|
Cours de Stevin, 1608 Catherine Philippe étudie ici le troisième livre Des triangles, chapitre de La Cosmographie, traduit en 1634, partie publiée en flamand en 1608.
Catalogue de cas Catherine Philippe étudie ici un extrait De L’histiodromie ou cours de Navires, une sous partie du quatrième livre La Géographie, chapitre de La Cosmographie, traduit en 1634, partie publiée en flamand en 1599 . Cet extrait |
| La navigation aux étoiles est une source inépuisable de problèmes de trigonométrie sphérique, parfois résolus par le truchement d’instruments... | |
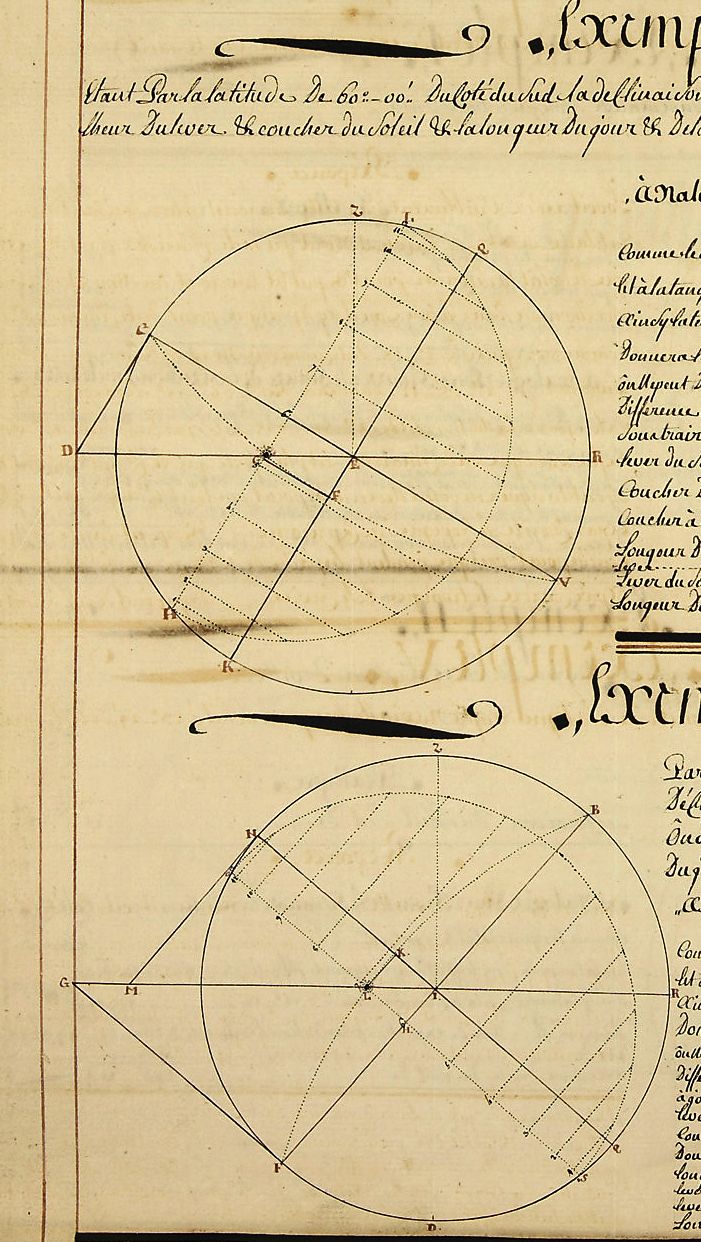 Manuscrit de Denoville, p. 196
|
Un manuscrit spécifique
Un livret de huit pages, inséré dans le manuscrit de Denoville, est consacré à la trigonométrie sphérique. Catherine Philippe en analyse le contenu. Les questions astronomiques Pour certaines des douze questions astronomiques qu’il considère, Denoville envisage plusieurs solutions, des démarches instrumentales par le quartier de réduction et par le quartier sphérique, et une démarche calculatoire par la trigonométrie sphérique. |